
Inhoudsopgave:
- Auteur Miles Stephen stephen@answers-science.com.
- Public 2024-01-18 08:17.
- Laatst gewijzigd 2025-01-22 17:06.
Hier, in stapformaat, is hoe een systeem op te lossen met drie vergelijkingen en drie variabelen:
- Kies twee paar vergelijkingen uit het systeem.
- Elimineer hetzelfde variabele van elk paar met behulp van de optellen/aftrekken-methode.
- Oplossen het stelsel van de twee nieuwe vergelijkingen met behulp van de methode optellen/aftrekken.
Ook om te weten is, hoe los je meerdere variabelen op?
Methode 2 Een lineaire vergelijking oplossen met eliminatie
- Kijk naar je vergelijking.
- Kies een variabele om te elimineren.
- Voeg de twee vergelijkingen toe of trek ze af om een van de variabelen te verwijderen en de andere variabele op te lossen.
- Sluit uw oplossing aan om de resterende variabele op te lossen.
Vervolgens is de vraag: hoe los je een stelsel van vergelijkingen op? Hier is hoe het gaat:
- Stap 1: Los een van de vergelijkingen voor een van de variabelen op. Laten we de eerste vergelijking voor y oplossen:
- Stap 2: Vervang die vergelijking door de andere vergelijking en los op voor x.
- Stap 3: Vervang x = 4 x = 4 x=4 in een van de oorspronkelijke vergelijkingen en los op voor y.
Ook gevraagd, wat zijn de 3 soorten variabelen?
De dingen die veranderen in een experiment heten variabelen . EEN variabele is een factor, eigenschap of aandoening die in verschillende hoeveelheden kan voorkomen of types . Een experiment heeft meestal: drie soorten variabelen : onafhankelijk, afhankelijk en gecontroleerd.
Hoe los je een stelsel vergelijkingen met twee variabelen op?
Tot systemen oplossen van algebraïsche vergelijkingen met twee variabelen , begin met het verplaatsen van de variabelen naar verschillende kanten van de vergelijking . Verdeel vervolgens beide zijden van de vergelijking door een van de variabelen tot oplossen daarom variabele . Neem vervolgens dat nummer en steek het in de formule om oplossen voor de andere variabele.
Aanbevolen:
Wat is een vergelijking met een of meer variabelen?

Algebraïsche vergelijking - Een vergelijking die een of meer variabelen bevat. Algebraïsche uitdrukking - Een uitdrukking die een of meer variabelen bevat. Coëfficiënt- Het getal dat wordt vermenigvuldigd met de variabele(n) in één term. In de term 67rt heeft rt een coëfficiënt van 67
Wat is een uitdrukking die een of meer variabelen bevat?
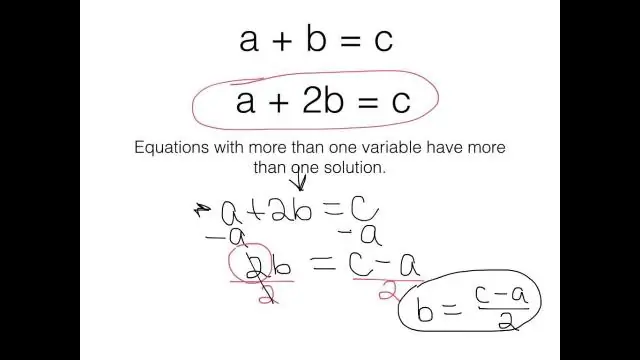
Een algebraïsche uitdrukking is een uitdrukking die een of meer variabelen bevat. Een algebraïsche vergelijking is een vergelijking die een of meer variabelen bevat
Hoe los je meerstapsvergelijkingen met variabelen op?

Om een dergelijke vergelijking op te lossen, moet je eerst de variabelen aan dezelfde kant van het gelijkteken krijgen. Voeg aan beide kanten -2,5j toe, zodat de variabele maar aan één kant blijft. Isoleer nu de variabele door 10,5 van beide kanten af te trekken. Vermenigvuldig beide zijden met 10 zodat 0,5y 5y wordt en deel vervolgens door 5
Hoe vereenvoudig je breuken met breuken en variabelen?

Belangrijkste stappen: Zoek de kleinste gemene deler (LCD) van alle noemers in de complexe breuken. Vermenigvuldig deze LCD met de teller en noemer van de complexe breuk. Vereenvoudig, indien nodig
Waarom evolueert een ster met een hoge massa anders dan een ster met een lage massa?

Waarom evolueert een ster met een hoge massa anders dan een ster met een lage massa? A) Het kan meer brandstoffen verbranden omdat de kern heter kan worden. Het heeft een lagere zwaartekracht, zodat het niet meer brandstof uit de ruimte kan halen
