
Inhoudsopgave:
- Auteur Miles Stephen stephen@answers-science.com.
- Public 2023-12-15 23:39.
- Laatst gewijzigd 2025-01-22 17:06.
De 68-95-99,7 regel stelt dat 68% van een de waarden van de normale verdeling zijn binnen één standaarddeviatie van het gemiddelde. 95% is binnen twee standaard afwijkingen en 99,7% zijn binnen drie standaard afwijkingen . Dat betekent dat de proportie van waarden binnen één standaarddeviatie is68/100 = 17/25.
Hoe vind je dan het percentage van één standaarddeviatie?
De empirische regel of 68-95-99,7% regel kan ons een goed startpunt geven. Deze regel vertelt ons dat ongeveer 68% van de gegevens zal vallen binnenin een standaardafwijking van het gemiddelde; ongeveer 95% zal dalen binnenin twee standaard afwijkingen van thema; en 99,7% zal dalen binnenin drie standaard afwijkingen van het gemiddelde.
Bovendien, welk percentage van de gegevens ligt binnen 2 standaarddeviaties van het gemiddelde? Voor een gegevens ingesteld met een symmetrische verdeling, ongeveer 68.3 procent van de waarden zal vallen binnenin een standaardafwijking van de gemeen , ongeveer 95,4 procent zal vallen binnen 2 standaarddeviaties van de gemeen , en ongeveer 99,7 procent zal vallen binnenin 3 standaard afwijkingen van de gemeen.
hoe vind je de standaarddeviatie van een steekproefomvang?
Laten we eerst de stappen bekijken voor het berekenen van de standaarddeviatie van het voorbeeld:
- Bereken het gemiddelde (eenvoudig gemiddelde van de getallen).
- Voor elk getal: trek het gemiddelde af.
- Tel alle gekwadrateerde resultaten bij elkaar op.
- Deel deze som door één minder dan het aantal gegevenspunten (N-1).
Wat is de formule voor standaarddeviatie?
De standaardafwijking wordt gegeven door de formule :s betekent ' standaardafwijking '. Trek nu het gemiddelde van elk van de gegeven getallen en het kwadraatresultaat afzonderlijk af. Dit komt overeen met de (x -)²stap.
Aanbevolen:
Hoe vind je standaarddeviatie en gemiddelde in Excel?
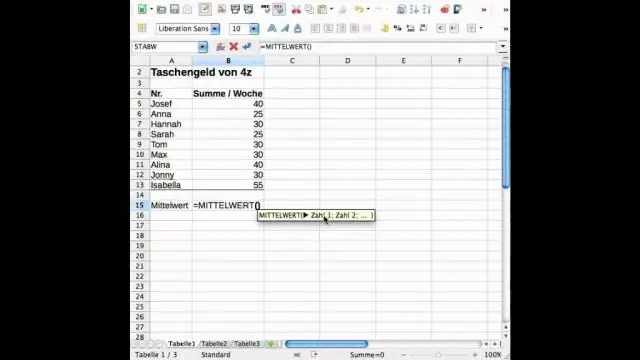
Standaarddeviatie is een maatstaf voor hoeveel variantie er is in een reeks getallen in vergelijking met het gemiddelde (gemiddelde) van de getallen. Om de standaarddeviatie in Excel te berekenen, kunt u een van de twee primaire functies gebruiken, afhankelijk van de gegevensset. Als de gegevens de gehele populatie vertegenwoordigen, kunt u de STDEV gebruiken. Pfunctie
Hoe vind je de standaarddeviatie van variabiliteit?

Om de standaarddeviatie te berekenen, telt u alle gegevenspunten bij elkaar op en deelt u deze door het aantal gegevenspunten, berekent u de variantie voor elk gegevenspunt en zoekt u vervolgens de vierkantswortel van de variantie
Hoe vind je de vergelijking van een lijn gegeven een punt en een parallelle lijn?

De vergelijking van de lijn in de vorm van het helling-snijpunt is y=2x+5. De helling van de parallellijn is hetzelfde: m=2. De vergelijking van de parallelle lijn is dus y=2x+a. Om a te vinden, gebruiken we het feit dat de lijn door het gegeven punt moet gaan:5=(2)⋅(&min;3)+a
Bij het vergelijken van twee populaties Hoe groter de standaarddeviatie, hoe meer spreiding?

Bij het vergelijken van twee populaties geldt: hoe groter de standaarddeviatie, hoe meer spreiding de verdeling heeft, op voorwaarde dat de variabele van belang dan de twee populaties dezelfde meetset heeft
Hoe zet je een procent om in een proportie?

Om 4/5 om te rekenen naar een percentage, stelt u de verhouding 4/5 = x%/100 in. Verhoudingen zullen kruisvermenigvuldigen. Vermenigvuldig de teller van de breuk links met de noemer van de breuk rechts: 4*100 = 400
