Video: Hoe verander je een functie in een hoekpuntvorm?
2024 Auteur: Miles Stephen | [email protected]. Laatst gewijzigd: 2023-12-15 23:39
Bekeren een kwadratisch van y = ax2 + bx + c vorm naar hoekpunt vorm , y = a(x - h)2+ k, je gebruikt het proces om het vierkant te voltooien. Laten we een voorbeeld bekijken. Overzetten y = 2x2 - 4x + 5 in hoekpuntvorm , en vermeld de hoekpunt . Vergelijking in y = ax2 + bx + c formulier.
Hoe converteert u in dit opzicht het intercept-formulier naar het vertex-formulier?
Overzetten y = 9x² - 12x + 1 tot onderscheppen vorm . Wij kunnen overzetten een kwadratische functie van standaard formulier , y = ax² + bx + c, naar de algemene hoekpunt vorm : y = a(x + p)² + q.
Bovendien, hoe vind je het hoekpunt? Stappen om op te lossen
- Verkrijg de vergelijking in de vorm y = ax2 + bx + c.
- Bereken -b / 2a. Dit is de x-coördinaat van het hoekpunt.
- Om de y-coördinaat van het hoekpunt te vinden, vult u eenvoudig de waarde van -b / 2a in de vergelijking voor x in en lost u op voor y. Dit is de y-coördinaat van het hoekpunt.
Wat is daarvan de onderscheppingsvorm van een parabool?
Samenvatting van de les. Nogmaals, de onderscheppen vorm van een parabool is y = a (x - r)(x - s), waarbij r en s de x- zijn onderschept , of waar de grafiek door de x-as gaat. Het voordeel van het gebruik van de onderscheppen vorm is dat je gemakkelijk de x- kunt vinden onderschept zonder factoring of met behulp van de kwadratische formule.
Wat is de vergelijking om het hoekpunt te vinden?
Parabolen hebben altijd een laagste punt (of een hoogste punt als de parabool ondersteboven staat). Dit punt, waar de parabool van richting verandert, wordt de " hoekpunt ". Als de kwadratische wordt geschreven in de vorm y = a(x - h)2 + k, dan de hoekpunt is het punt (h, k).
Aanbevolen:
Hoe bepaal je of een functie een horizontale raaklijn heeft?
Horizontale lijnen hebben een helling van nul. Daarom, wanneer de afgeleide nul is, is de raaklijn horizontaal. Om horizontale raaklijnen te vinden, gebruikt u de afgeleide van de functie om de nullen te lokaliseren en deze weer in de oorspronkelijke vergelijking in te vullen
Hoe verander ik een oppervlak in een polylijn in AutoCAD?
Re: Oppervlaktegrens omzetten in polylijn Zet uw rand aan binnen uw oppervlaktestijl, selecteer oppervlak en binnen het contextuele lint is er een pictogram voor uitpakken van objecten, dan verschijnt er een dialoogvenster met de vraag wat u wilt extraheren. Schakel alles uit behalve de rand, druk op ok
Hoe bepaal je of een relatie een functie in een grafiek is?
ANTWOORD: Voorbeeldantwoord: U kunt bepalen of elk element van het domein is gekoppeld aan precies één element van het bereik. Als u bijvoorbeeld een grafiek krijgt, kunt u de verticale lijntest gebruiken; als een verticale lijn de grafiek meer dan eens snijdt, dan is de relatie die de grafiek voorstelt geen functie
Hoe verander je een vaste stof in een vloeistof?
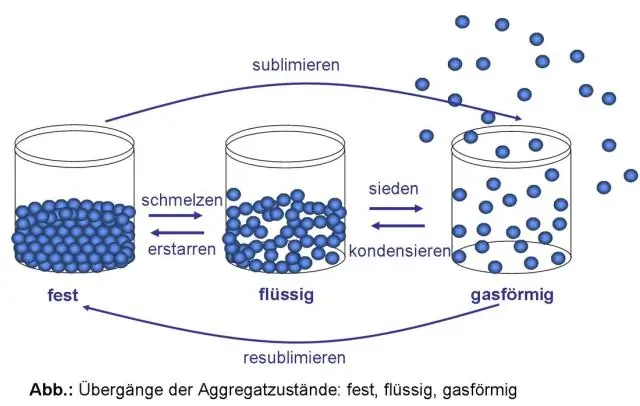
De atomen in een vloeistof hebben meer energie dan de atomen in een vaste stof. Er is een speciale temperatuur voor elke stof die het smeltpunt wordt genoemd. Wanneer een vaste stof de temperatuur van zijn smeltpunt bereikt, kan het een vloeistof worden
Hoe weet je of een functie geen functie is?
Bepalen of een relatie een functie in een grafiek is, is relatief eenvoudig met behulp van de verticale lijntest. Als een verticale lijn de relatie op de grafiek slechts één keer op alle locaties kruist, is de relatie een functie. Als een verticale lijn de relatie echter meer dan eens kruist, is de relatie geen functie