Video: Hoe schrijf je een Biconditional als twee conditionals?
2024 Auteur: Miles Stephen | [email protected]. Laatst gewijzigd: 2023-12-15 23:39
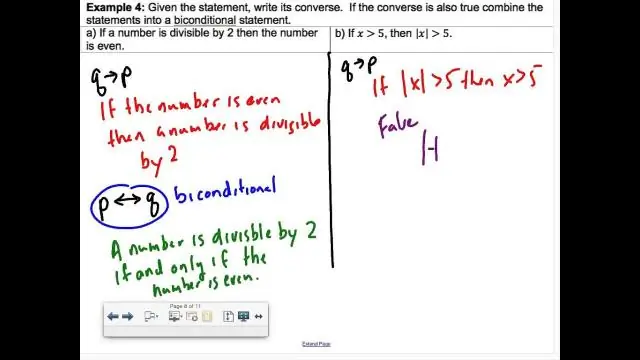
Het is een combinatie van twee voorwaardelijk uitspraken, “als twee lijnsegmenten congruent zijn dan zijn ze even lang” en “if twee lijnsegmenten even lang zijn, dan zijn ze congruent”. EEN biconditioneel is waar dan en slechts dan als zowel de voorwaarden zijn waar. Bi- voorwaarden worden weergegeven door het symbool ↔ of ⇔.
Bovendien, wanneer kunt u een Biconditional-verklaring schrijven?
Wanneer jij combineer een voorwaardelijke uitspraak en het omgekeerde, jij Maak een bivoorwaardelijke verklaring . EEN bivoorwaardelijke verklaring is een uitspraak Dat kan worden geschreven in de vorm "p als en slechts als q." Dit betekent "als p, dan q" en "als q, dan p." De biconditioneel “p als en slechts als q” kan ook worden geschreven als “p iff q” of p ? Q.
Bovendien, is alleen als een Biconditional? INDIEN EN ALLEEN ALS , is een biconditioneel bewering, wat betekent dat beide beweringen waar zijn of beide onwaar. Het is dus in wezen en “ INDIEN ” verklaring die twee kanten op werkt.
Ook om te weten, wat zijn voorwaardelijke en bivoorwaardelijke uitspraken?
Wanneer we twee combineren Voorwaardelijke stellingen op deze manier hebben we een biconditioneel . Definitie: A bivoorwaardelijke verklaring wordt gedefinieerd als waar wanneer beide delen dezelfde waarheidswaarde hebben. In de bovenstaande waarheidstabel is p q waar als p en q dezelfde waarheidswaarden hebben (d.w.z. wanneer beide waar zijn of beide onwaar).
Wat is een voorbeeld van een Biconditional-statement?
Voorbeelden van bivoorwaardelijke verklaringen De bivoorwaardelijke uitspraken voor deze twee verzamelingen zou zijn: De veelhoek heeft slechts vier zijden dan en slechts dan als de veelhoek een vierhoek is. De veelhoek is een vierhoek dan en slechts dan als de veelhoek maar vier zijden heeft.
Aanbevolen:
Hoe schrijf je een vergelijking in punthellingvorm gegeven twee punten?
Er zijn verschillende vormen waarmee we de vergelijking van een lijn kunnen schrijven: de punt-hellingvorm, de helling-snijvorm, de standaardvorm, enz. De vergelijking van een lijn gegeven twee punten (x1, y1) en (x2, y2 ) waardoor de lijn gaat, wordt gegeven door, ((y - y1)/(x - x1)) / ((y2 - y1)/(x2 - x1))
Hoe schrijf je 13/4 als een gemengd getal?
Als een negatieve onechte breuk (|teller| > |noemer|): - 13/4 = - 13/4 Als een gemengd getal. (een geheel getal en een eigen breuk, van hetzelfde teken): - 13/4 = - 3 1/4 Als percentage: - 13/4 = - 325%
Hoe schrijf je een breuk als een product van een geheel getal en een eenheidsbreuk?
Regels om het product van een eenheidsbreuk en een geheel getal te vinden We schrijven het gehele getal eerst als een breuk, d.w.z. door het te delen door één; bijvoorbeeld: 7 wordt geschreven als 71. We vermenigvuldigen dan de tellers. We vermenigvuldigen de noemers. Als er een vereenvoudiging nodig is, is het klaar en dan schrijven we de laatste breuk
Hoe schrijf je als een breuk in de eenvoudigste vorm?
Bij het schrijven van breuken in de eenvoudigste vorm zijn er twee regels die u moet volgen: Vraag of de teller en de noemer kunnen worden gedeeld door hetzelfde getal, dat een gemeenschappelijke factor wordt genoemd. Kijk of ten minste één getal in de breuk een priemgetal is
Hoe schrijf je een vergelijking in de vorm van een hellingsintercept voor een tabel?
Neem de vergelijking y = mx + b en vul de m-waarde (m = 1) en een paar (x, y) coördinaten uit de tabel in, zoals (5, 3). Los dan op voor b. Gebruik ten slotte de gevonden m- en b-waarden (m = 1 en b = -2) om de vergelijking te schrijven