Inhoudsopgave:
Video: Kunnen we regressie uitvoeren op niet-lineaire gegevens?
2024 Auteur: Miles Stephen | [email protected]. Laatst gewijzigd: 2023-12-15 23:39
Niet-lineaire regressie kan passen op veel meer soorten rondingen, maar het is kan meer inspanning vergen, zowel om de beste pasvorm te vinden als om interpreteren de rol van de onafhankelijke variabelen. Bovendien is R-kwadraat niet geldig voor niet-lineaire regressie en het is onmogelijk om berekenen p-waarden voor de parameterschattingen.
Kan een regressie op deze manier niet-lineair zijn?
In statistieken, niet-lineaire regressie is een vorm van regressie analyse waarin waarnemingsgegevens worden gemodelleerd door een functie die a niet-lineair combinatie van de modelparameters en is afhankelijk van een of meer onafhankelijke variabelen. De gegevens worden gefit door een methode van opeenvolgende benaderingen.
Men kan zich ook afvragen, is r alleen kwadraat voor lineaire regressie? Het algemene wiskundige kader voor R - kwadraat werkt niet correct als de regressie model is niet lineair . Ondanks dit probleem berekent de meeste statistische software nog steeds R - kwadraat voor niet-lineaire modellen. Als je gebruikt R - kwadraat om de beste te kiezen model -, het leidt tot de juiste alleen model 28-43% van de tijd.
Hoe bereken je in dit verband niet-lineaire regressie?
Als uw model een vergelijking in de vorm Y = a0 + b1x1, het is een lineaire regressie model. Zo niet, dan is het niet-lineair.
Y = f(X,) + ε
- X = een vector van p-voorspellers,
- β = een vector van k parameters,
- f(-) = een bekende regressiefunctie,
- ε = een foutterm.
Wat zijn de soorten regressie?
Soorten regressie
- Lineaire regressie. Het is de eenvoudigste vorm van regressie.
- Polynomiale regressie. Het is een techniek om een niet-lineaire vergelijking te passen door polynoomfuncties van een onafhankelijke variabele te nemen.
- Logistieke regressie.
- Kwantiele regressie.
- Rug regressie.
- Lasso-regressie.
- Elastische netto regressie.
- Belangrijkste componenten regressie (PCR)
Aanbevolen:
Welke organismen kunnen fotosynthese en cellulaire ademhaling uitvoeren?
Planten die aan licht worden blootgesteld, voeren zowel fotosynthese als cellulaire ademhaling uit. Na enige tijd in het donker zal in de planten alleen cellulaire ademhaling optreden. Tijdens de fotosynthese geven planten zuurstof af. Tijdens cellulaire ademhaling geven planten koolstofdioxide af
Wat zijn niet-gegroepeerde gegevens in statistieken?
Niet-gegroepeerde gegevens zijn de gegevens die u voor het eerst verzamelt uit een experiment of onderzoek. De gegevens zijn onbewerkt - dat wil zeggen, ze zijn niet gesorteerd in categorieën, geclassificeerd of anderszins gegroepeerd. Een niet-gegroepeerde set gegevens is in feite een lijst met getallen
Welk kenmerk van gegevens is een maat voor de hoeveelheid die de gegevens zeer waarderen?
Variatie: een maatstaf voor de mate waarin de gegevenswaarden variëren. ? Distributie: de aard of vorm van de spreiding van de gegevens over het waardenbereik (zoals klokvormig). ? Uitbijters: steekproefwaarden die ver van de overgrote meerderheid van de andere steekproefwaarden liggen
Welke soorten gegevens kunnen het beste worden gemeten met een Isoline-kaart?
Definitie. De isoline-representatie is de meest gebruikte methode om kwantitatieve verschijnselen te visualiseren die zich integraal voordoen en waarvan de waarden continu in de ruimte variëren. Ze worden daarom continua genoemd. Voorbeelden van dergelijke continua zijn temperatuur, luchtdruk, neerslaghoogten of grondhoogten
Wat zijn de maten van centrale tendens voor niet-gegroepeerde gegevens?
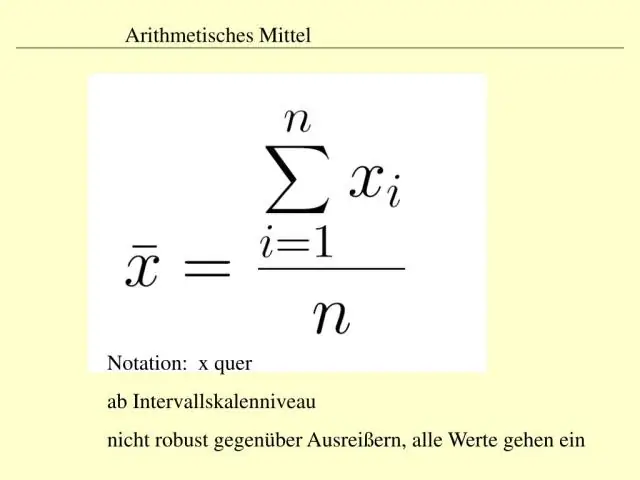
De term centrale tendens verwijst naar de middelste of typische waarde van een reeks gegevens, die meestal wordt gemeten met behulp van de drie m's: gemiddelde, mediaan en modus. Het gemiddelde, de mediaan en de modus staan bekend als de maten van de centrale tendens