
- Auteur Miles Stephen [email protected].
- Public 2023-12-15 23:39.
- Laatst gewijzigd 2025-01-22 17:06.
Voorbeeld 1 Bepaal of de volgende reeks convergent is of afwijkend . Deze functie is duidelijk positief en als we x x de noemer groter maken zullen groter worden en dus neemt de functie ook af. De integraal is afwijkend en zo is de serie ook afwijkend Door de Integrale test.
Is e x daarnaast convergent of divergent?
1/( ex ) is groter of gelijk aan 1/( ex +1) (tussen nul en oneindig) Onjuiste integraal ∫∞01( ex )NS x is convergerend en het is echter 1 oneigenlijke integraal ∫∞01( ex +1)d x is afwijkend.
Men kan zich ook afvragen, wat is ongepast integraal met voorbeeld? Een Onjuist integraal is zeker integraal die een of beide limieten oneindig heeft of een integrand die oneindig nadert op een of meer punten in het integratiebereik. Onjuiste integralen kan niet worden berekend met een normale Riemann integraal . Voor voorbeeld , de integraal.
Ten tweede, wat is convergentie en divergentie in calculus?
Serie Convergentie en divergentie - Definities Een reeks Σa convergeert naar een som S als en slechts als de reeks partiële sommen convergeert naar S. Dat wil zeggen, een reeks convergeert als de volgende limiet bestaat: Anders, als de limiet van sk (als k → ∞) oneindig is of niet bestaat, dan divergeert de reeks.
Wat is de waarde van 1 oneindig?
Eigenlijk, 1 gedeeld door een heel groot getal komt heel dicht bij nul, dus… 1 gedeeld door oneindigheid , als je echt zou kunnen bereiken oneindigheid , is gelijk aan 0.
Aanbevolen:
Wat zegt Mauchly's test van bolvormigheid je?

Mauchly, Mauchly's test van sfericiteit is een populaire test om te evalueren of de sfericiteitsveronderstelling is geschonden. De nulhypothese van bolvormigheid en alternatieve hypothese van niet-bolvormigheid in het bovenstaande voorbeeld kan wiskundig worden geschreven in termen van verschilscores
Hoe doe je de Durbin Watson-test in Minitab?
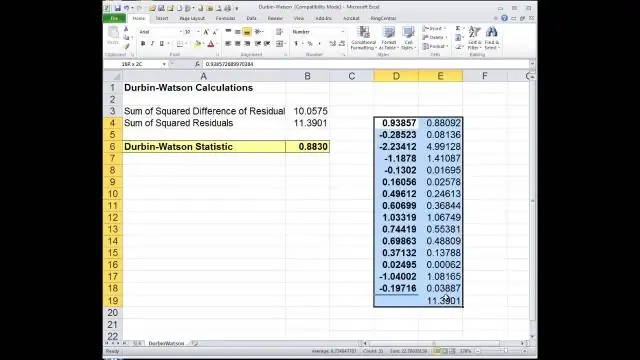
In Minitab: Klik op Statistiek > Regressie > Regressie > Regressiemodel passen. Klik op 'Resultaten' en controleer de Durbin-Watson-statistiek
Wat is het verschil tussen gradiënt en divergentie?

2 antwoorden. De gradiënt is de directionele veranderingssnelheid van een scalaire functie in Rn, terwijl de divergentie de hoeveelheid output versus input meet voor een eenheidsvolume van een vector gewaardeerde 'flow' in Rn
Wat is het verschil tussen een gepaarde t-test en een t-test met 2 steekproeven?

T-toets met twee steekproeven wordt gebruikt wanneer de gegevens van twee steekproeven statistisch onafhankelijk zijn, terwijl de gepaarde t-toets wordt gebruikt wanneer gegevens de vorm hebben van gematchte paren. Om de t-test met twee steekproeven te gebruiken, moeten we aannemen dat de gegevens van beide steekproeven normaal verdeeld zijn en dat ze dezelfde varianties hebben
Hoe kan de streak-test nuttig zijn bij het identificeren van mineralen?

De 'streaktest' is een methode om de kleur van een mineraal in poedervorm te bepalen. De streeptest wordt gedaan door een monster van het mineraal over een stuk ongeglazuurd porselein te schrapen dat bekend staat als een 'streepplaat'. Dit kan een kleine hoeveelheid mineraalpoeder op het oppervlak van de plaat produceren
