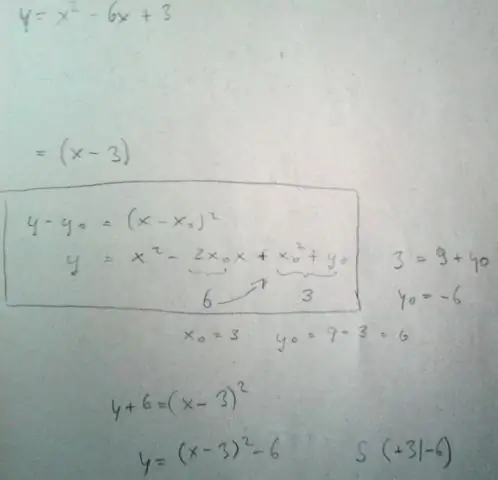
- Auteur Miles Stephen stephen@answers-science.com.
- Public 2023-12-15 23:39.
- Laatst gewijzigd 2025-06-01 05:05.
EEN kwadratische functie is een van de vorm f(x) = ax2 + bx + c, waarbij a, b en c getallen zijn waarvan a niet gelijk is aan nul. De grafiek van a kwadratische functie is een kromme die een parabool wordt genoemd. Parabolen kunnen naar boven of naar beneden openen en variëren in "breedte" of "steilheid", maar ze hebben allemaal dezelfde basis "U"-vorm.
Hiervan, WAT IS A in topvorm?
y = a(x - h)2 + k, waarbij (h, k) de. is hoekpunt . De "a" in de hoekpunt vorm is dezelfde "a" als. in y = ax2 + bx + c (dat wil zeggen, beide a's hebben exact dezelfde waarde). Het teken op "a" geeft aan of de kwadratische opening omhoog of omlaag gaat.
hoe bepaal je dat een vergelijking een functie is? Het is relatief eenvoudig om bepalen of een vergelijking is een functie door op te lossen voor y. Wanneer u een vergelijking en een specifieke waarde voor x, zou er maar één corresponderende y-waarde voor die x-waarde moeten zijn. Bijvoorbeeld, y = x + 1 is a functie omdat y altijd één groter is dan x.
Hoe schrijf je op deze manier een vergelijking voor een parabool?
Voor parabolen die zijwaarts openen, de standaardvorm vergelijking is (y - k)^2 = 4p(x - h). Het hoekpunt of de punt van onze parabool wordt gegeven door het punt (h, k). Voor parabolen die op en neer opengaan, wordt het focuspunt gegeven door (h, k + p). Voor parabolen die zijwaarts openen, is het focuspunt (h + p, k).
Wat is de standaardvorm van een kwadratische functie?
EEN kwadratische functie is een functie van graad twee. De grafiek van a kwadratische functie is een parabool . De algemene vorm van een kwadratische functie is f(x)=ax2+bx+c waarbij a, b en c reële getallen zijn en a≠0. De standaardvorm van een kwadratische functie is f(x)=a(x−h)2+k.
Aanbevolen:
Hoe los je een kwadratische vergelijking op met behulp van de nulfactorwet?

Hieruit kunnen we afleiden dat: Als het product van twee willekeurige getallen nul is, dan is één of beide getallen nul. Dat wil zeggen, als ab = 0, dan is a = 0 of b = 0 (inclusief de mogelijkheid dat a = b = 0). Dit wordt de nulfactorwet genoemd; en we gebruiken het vaak om kwadratische vergelijkingen op te lossen
Wat is een voorbeeld van een kwadratische vergelijking?

Een kwadratische vergelijking is een vergelijking van de tweede graad, wat betekent dat het ten minste één kwadraat bevat. De standaardvorm is ax² + bx + c = 0 waarbij a, b en c constanten zijn, of numerieke coëfficiënten, en x is een onbekende variabele. Een absolute regel is dat de eerste constante 'a' geen nul kan zijn
Hoe ziet de grafiek van een kwadratische vergelijking eruit?

De grafiek van een kwadratische functie is een U-vormige kromme die een parabool wordt genoemd. Het kan worden getekend door oplossingen voor de vergelijking te plotten, door het hoekpunt te vinden en de symmetrieas te gebruiken om geselecteerde punten te plotten, of door de wortels en het hoekpunt te vinden. De standaardvorm van een kwadratische vergelijking is
Hoe converteer je een kwadratische vergelijking van hoekpunt naar rekenmachine?

Calculator voor de conversie van de basisvorm naar de topvorm y=x2+3x+5. x2+3x+5= || +(p2)2-(p2)2=0. || a2+2ab+b2=(a+b)2. || -1⋅-1=+1. xS=-32=-1,5. yS=-(32)2+5=2,75
Hoe converteer je een kwadratische vergelijking van algemene vorm naar standaardvorm?

Elke kwadratische functie kan worden geschreven in de standaardvorm f(x) = a(x - h) 2 + k waarbij h en k worden gegeven in termen van coëfficiënten a, b en c. Laten we beginnen met de kwadratische functie in algemene vorm en het vierkant voltooien om het in standaardvorm te herschrijven
