Video: Wat is een voorbeeld van een kwadratische vergelijking?
2024 Auteur: Miles Stephen | [email protected]. Laatst gewijzigd: 2023-12-15 23:39
EEN kwadratische vergelijking is een vergelijking van de tweede graad, wat betekent dat het ten minste één kwadraat bevat. De standaardvorm is ax² + bx + c = 0 waarbij a, b en c constanten zijn, of numerieke coëfficiënten, en x is een onbekende variabele. Een absolute regel is dat de eerste constante "a" geen nul kan zijn.
Ook om te weten is, wat is een voorbeeld van een kwadratische functie?
enkele veel voorkomende voorbeelden van de kwadratische functie Merk op dat de grafiek van de kwadratische functie is een parabool. Dit betekent dat het een bocht is met een enkele hobbel. De grafiek is symmetrisch om een lijn die de symmetrie-as wordt genoemd. Het punt waar de symmetrieas de parabool snijdt, staat bekend als het hoekpunt.
Weet ook, wat is a in een kwadratische vergelijking? In de algebra, a kwadratische vergelijking (van het Latijnse quadratus voor "vierkant") is any vergelijking die in standaardvorm kan worden herschikt als. waarbij x staat voor een onbekende, en a, b en c staan voor bekende getallen, waarbij a ≠ 0. Als a = 0, dan is de vergelijking is lineair, niet kwadratisch , want er is geen. termijn.
Mensen vragen ook, wat is kwadratische vergelijking en geven voorbeelden?
De standaardvorm van a kwadratisch is y = ax^2 + bx + c, waarbij a, b en c getallen zijn en a niet 0 kan zijn. Voorbeelden van kwadratische vergelijkingen omvatten al deze: y = x ^ 2 + 3x + 1.
Wat zijn de 3 vormen van kwadratische functies?
Hoewel de meeste manieren om de. te schrijven kwadratisch vergelijking overbodig en nutteloos zijn, zijn er drie vormen die eigenlijk unieke toepassingen hebben. Deze drie hoofd formulieren waaruit we parabolen tekenen, worden standaard genoemd formulier , onderscheppen formulier en hoekpunt formulier.
Aanbevolen:
Hoe los je een kwadratische vergelijking op met behulp van de nulfactorwet?
Hieruit kunnen we afleiden dat: Als het product van twee willekeurige getallen nul is, dan is één of beide getallen nul. Dat wil zeggen, als ab = 0, dan is a = 0 of b = 0 (inclusief de mogelijkheid dat a = b = 0). Dit wordt de nulfactorwet genoemd; en we gebruiken het vaak om kwadratische vergelijkingen op te lossen
Wat is de vergelijking van de kwadratische functie?
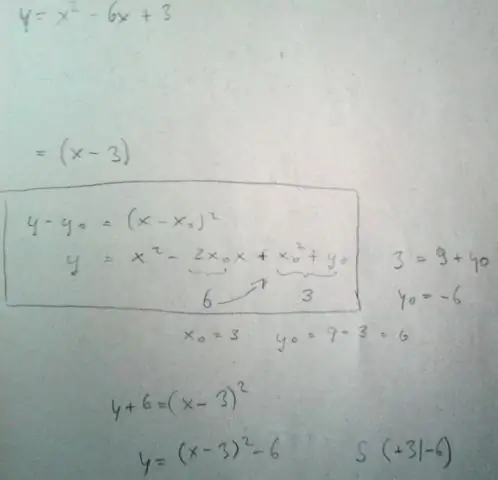
Een kwadratische functie is een van de vorm f(x) = ax2 + bx + c, waarbij a, b en c getallen zijn waarvan a niet gelijk is aan nul. De grafiek van een kwadratische functie is een kromme die een parabool wordt genoemd. Parabolen kunnen naar boven of naar beneden openen en variëren in 'breedte' of 'steilheid', maar ze hebben allemaal dezelfde basis 'U'-vorm
Hoe ziet de grafiek van een kwadratische vergelijking eruit?
De grafiek van een kwadratische functie is een U-vormige kromme die een parabool wordt genoemd. Het kan worden getekend door oplossingen voor de vergelijking te plotten, door het hoekpunt te vinden en de symmetrieas te gebruiken om geselecteerde punten te plotten, of door de wortels en het hoekpunt te vinden. De standaardvorm van een kwadratische vergelijking is
Hoe converteer je een kwadratische vergelijking van hoekpunt naar rekenmachine?
Calculator voor de conversie van de basisvorm naar de topvorm y=x2+3x+5. x2+3x+5= || +(p2)2-(p2)2=0. || a2+2ab+b2=(a+b)2. || -1⋅-1=+1. xS=-32=-1,5. yS=-(32)2+5=2,75
Hoe converteer je een kwadratische vergelijking van algemene vorm naar standaardvorm?
Elke kwadratische functie kan worden geschreven in de standaardvorm f(x) = a(x - h) 2 + k waarbij h en k worden gegeven in termen van coëfficiënten a, b en c. Laten we beginnen met de kwadratische functie in algemene vorm en het vierkant voltooien om het in standaardvorm te herschrijven