- Auteur Miles Stephen stephen@answers-science.com.
- Public 2023-12-15 23:39.
- Laatst gewijzigd 2025-06-01 05:05.
In de statistieken is de 68 - 95 - 99,7 regel , ook bekend als de empirische regel , is een afkorting gebruikt om het percentage waarden te onthouden dat binnen een band rond het gemiddelde ligt in een normale verdeling met een breedte van respectievelijk twee, vier en zes standaarddeviaties; nauwkeuriger, 68,27%, 95,45% en 99,73% van de waarden liggen
Wat is in dit verband de 95 procent-regel?
de empirische regel stelt dat voor een normale verdeling bijna alle gegevens binnen drie standaarddeviaties van het gemiddelde zullen vallen. 95 % valt binnen twee standaarddeviaties. 99,7% valt binnen drie standaarddeviaties.
Weet ook, wat zijn de 68% 95% en 99,7% betrouwbaarheidsintervallen voor de steekproefgemiddelden? Sinds 95 % van de waarden valt binnen twee standaarddeviaties van de gemeen volgens de 68 - 95 - 99.7 Regel, voeg eenvoudig twee standaarddeviaties toe aan en trek ze af van de gemeen om de 95 % Betrouwbaarheidsinterval . Volgens de 68 - 95 - 99.7 Regel: ➢ De 68 % Betrouwbaarheidsinterval voor deze voorbeeld ligt tussen 78 en 82.
Ook om te weten is, waarom is de standaarddeviatie 68 procent?
Zoals anderen al hebben gezegd, is het een resultaat van calculus dat deze formule berekend is als een integraal van -1/2 sigma tot 1/2 sigma (voor 1 sigma = 1 standaardafwijking ) resulteert in een gebied onder de curve van 0,68, waarbij het hele gebied, berekend als integraal van -oneindig tot +oneindig 1, is, dus je krijgt 68 % voor één standaard
Wat is 95 procent betrouwbaarheidsinterval?
EEN 95 % Betrouwbaarheidsinterval is een reeks waarden die u kunt zijn 95 % zeker bevat het werkelijke gemiddelde van de populatie. Met de kleine steekproef aan de linkerkant, de 95 % Betrouwbaarheidsinterval is vergelijkbaar met het bereik van de gegevens.
Aanbevolen:
Hoe gebruik je een Sperry DM210a?

Een Sperry DM 210A-meter gebruiken Steek het zwarte meetsnoer in de COM-aansluiting en het rode meetsnoer in de V-ohm-aansluiting. Zet de bereikkeuzeschakelaar op de meter op 600 DCV om gelijkspanning te meten of op 600 ACV voor wisselspanning. Raak de zwarte testkabel aan op aarde en de rode kabel op een punt op het circuit
Hoe gebruik je transformatie in een zin?

Transform Zin Voorbeelden We hebben in duizenden jaren nog nooit een vampier in een mens kunnen veranderen. Wesley geloofde dat de genade van God elk leven dat het ontving kon transformeren. Haar beleid was tot voor kort om ze om te zetten in Frans grondgebied
Hoe gebruik je een collimator?
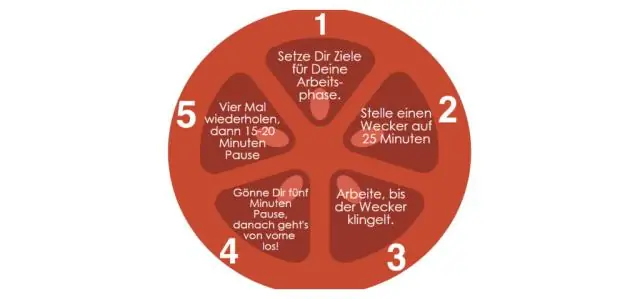
Een collimator is een apparaat dat een bundel deeltjes of golven vernauwt. Versmallen kan betekenen dat de bewegingsrichtingen meer uitgelijnd worden in een specifieke richting (d.w.z. gecollimeerd licht of parallelle stralen maken), of dat de ruimtelijke dwarsdoorsnede van de bundel kleiner wordt (straalbeperkend apparaat)
Hoe gebruik je oude weegschalen?

Het uiteinde van de balk helemaal links van de schaal moet naar de bovenkant van het frame stijgen. Het zal meestal de top raken met een duidelijke bult. Verplaats het grote schuifgewicht van inkeping naar inkeping naar rechts. Het uiteinde van de balk, dat uitsteekt aan de linkerkant van de schaal, zal zakken als u het gewicht verplaatst
Wanneer gebruik je de activiteitenreeks hoe gebruik je hem?

Het wordt gebruikt om de producten van enkelvoudige verplaatsingsreacties te bepalen, waarbij metaal A een ander metaal B in een oplossing zal vervangen als A hoger in de reeks is. Activiteitenreeksen van enkele van de meest voorkomende metalen, gerangschikt in aflopende volgorde van reactiviteit
