Inhoudsopgave:
Video: Hoe doe je de shell-methode in calculus?
2024 Auteur: Miles Stephen | [email protected]. Laatst gewijzigd: 2023-12-15 23:39
De shell-methode: berekent het volume van het volledige omwentelingslichaam door de volumes van deze dunne cilindrische schalen bij elkaar op te tellen als de dikte Δ x Delta x Δx naar 0 0 0 gaat in de limiet: V = ∫ d V = ∫ ab 2 π xydx = ∫ ab 2 π xf (x) dx. V = int dV = int_a^b 2 pi x y, dx = int_a^b 2 pi x f(x), dx.
Zo ja, wat is de formule van de Shell-methode?
De shell-methode: vertrouwt op een eenvoudige geometrische formule . Een zeer dunne cilindrische schelp kan worden benaderd door een zeer dunne rechthoekige vaste stof. Dus het volume van de schelp wordt benaderd door het volume van het prisma, namelijk L x B x H = (2 r) x h x dr = 2πrh dr.
Bovendien, wat is de schijfmethode-formule? Met andere woorden (minder kleurrijke woorden), de schijf methode: is het proces van het vinden van het volume van een object door dat object te verdelen in vele kleine cilinders/ schijven en dan het toevoegen van de volumes van deze kleine schijven samen. De straal van de cilinder wordt gegeven door een functie f(x) en de hoogte is de verandering in x.
Evenzo vragen mensen: hoe gebruik je de wasmachine-methode in calculus?
Hoe u het volume van een vorm kunt vinden met behulp van de ringmethode
- Bepaal waar de twee krommen elkaar snijden. Dus de betreffende vaste stof overspant het interval op de x-as van 0 tot 1.
- Figuur het gebied van een dwarsdoorsnede wasmachine.
- Vermenigvuldig dit gebied met de dikte, dx, om het volume van een representatieve ring te krijgen.
- Tel de volumes van de ringen op van 0 tot 1 door te integreren.
Wat is de cilindrische schaalmethode?
De cilindrische schaalmethode: . Gebruik de shell-methode: om het volume van de vaste stof te berekenen die is uitgetekend door het gebied dat wordt begrensd door de x-as te roteren, de curve y = x3 en de lijn x = 2 om de y-as. Hier y = x3 en de limieten lopen van x = 0 tot x = 2.
Aanbevolen:
Hoe doe je de Durbin Watson-test in Minitab?
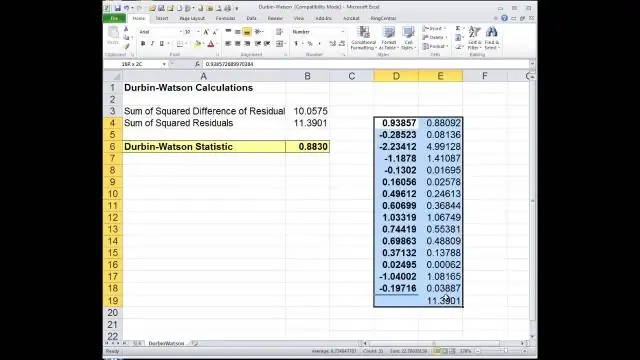
In Minitab: Klik op Statistiek > Regressie > Regressie > Regressiemodel passen. Klik op 'Resultaten' en controleer de Durbin-Watson-statistiek
Hoe doe je stelsel van vergelijkingen woordproblemen?
Om een stelsel van vergelijkingswoordproblemen op te lossen, definiëren we eerst de variabelen en extraheren we de vergelijkingen uit de woordproblemen. We kunnen het systeem dan oplossen met behulp van grafische, eliminatie- of substitutiemethoden
Is multivariabele calculus hetzelfde als calculus 3?
Bereken 2 = integraalberekening. Calc 3 = multivariabele calculus = vectoranalyse. Een semester voornamelijk bezig met partiële afgeleiden, oppervlakte-integralen, dat soort dingen
Hoe doe je waarschijnlijkheid samengestelde gebeurtenissen?
Het bepalen van de waarschijnlijkheid van een samengestelde gebeurtenis omvat het vinden van de som van de kansen van de afzonderlijke gebeurtenissen en, indien nodig, het verwijderen van overlappende kansen. Een exclusieve samengestelde gebeurtenis is een gebeurtenis waarin de meerdere gebeurtenissen elkaar niet overlappen. In wiskundige termen: P(C) = P(A) + P(B)
Hoe doe je een eenvoudige continuïteitstester?
VIDEO De vraag is ook, wat is een eenvoudige continuïteitstester? EEN continuïteitstester is een eenvoudig apparaat bestaande uit twee testsondes en een licht (LED) of zoemerindicator. Het wordt gebruikt om de aanwezigheid van continuïteit of een breuk tussen de twee uiteinden van een geleider die is verbonden met de testsondes.