Video: Hoe weet je of een transformatie één op één is?
2024 Auteur: Miles Stephen | [email protected]. Laatst gewijzigd: 2023-12-15 23:39
Wanneer een lineaire transformatie wordt beschreven in termen van een matrix is het gemakkelijk om bepalen of de lineaire transformatie is één-op-één of niet door de lineaire afhankelijkheid van de kolommen van de matrix te controleren. Indien de kolommen zijn lineair onafhankelijk, de lineaire transformatie is één-op-één.
Wat betekent het in dit verband als een lineaire transformatie één op één is?
Eén-op-één lineaire transformaties . Definitie : EEN lineaire transformatie die verschillende punten/vectoren in kaart brengt van naar verschillende punten/vectoren in heet a een-op-een transformatie of een injectieve transformatie . Dus voor elke vector bestaat er precies een vector zodanig dat.
Je kunt je ook afvragen, kan een lineaire transformatie wel op zijn, maar niet één op één? In matrixtermen betekent dit dat a transformatie met matrix A is op als Ax=b een oplossing heeft voor elke b in het bereik. Als een transformatie is op maar niet één-op-één , jij kan denk dat het domein te veel vectoren heeft om in het bereik te passen.
Hiervan, kan een matrix één op één zijn en niet op?
In het bijzonder de enige matrices Dat kan beide zijn een op een en op zijn vierkant matrices . Aan de andere kant, jij kan hebben een m×n Matrix met m<n dat is op , of een dat is niet op . En jij kan heb m×n matrices met m>n dat zijn een op een , en matrices dat zijn niet één op één.
Hoe bewijs je een lineaire transformatie?
Voor elke y ∈ Y is er minstens één x ∈ X met f(x) = y. Elk element van het codomein van f is een uitvoer voor een invoer. We kunnen detecteren of een lineaire transformatie is één-op-één of op door de kolommen van de standaardmatrix te inspecteren (en rijreductie).
Aanbevolen:
Hoe weet je of een transformatie een dilatatie is?
Een beschrijving van een dilatatie omvat de schaalfactor (of ratio) en het midden van de dilatatie. Het centrum van dilatatie is een vast punt in het vlak. Als de schaalfactor groter is dan 1, is de afbeelding een vergroting (een rek). Als de schaalfactor tussen 0 en 1 ligt, is de afbeelding een verkleining (een krimp)
Hoe beschrijf je transformatie in bacteriën?
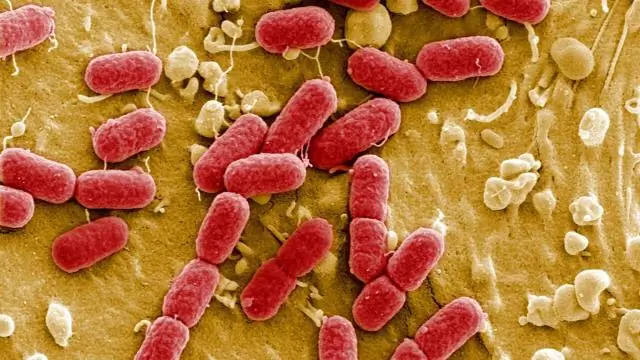
Het stukje DNA of gen van belang wordt uit zijn oorspronkelijke DNA-bron gesneden met behulp van een restrictie-enzym en vervolgens door ligatie in het plasmide geplakt. Het plasmide dat het vreemde DNA bevat, is nu klaar om in bacteriën te worden ingebracht. Dit proces heet transformatie
Hoe gebruik je transformatie in een zin?
Transform Zin Voorbeelden We hebben in duizenden jaren nog nooit een vampier in een mens kunnen veranderen. Wesley geloofde dat de genade van God elk leven dat het ontving kon transformeren. Haar beleid was tot voor kort om ze om te zetten in Frans grondgebied
Hoe bepaalden Avery en zijn groep welk molecuul het belangrijkst was voor transformatie?
Beschrijf in het kort hoe Avery en zijn groep bepaalden welk molecuul het belangrijkst was voor transformatie. Avery en zijn groep gebruikten twee verschillende enzymen op een extract van door hitte gedode bacteriën. De ene vernietigde DNA, de andere vernietigde alles behalve. Ze ontdekten dat transformatie nog steeds plaatsvond als DNA aanwezig was
Hoe beschrijf je een enkele transformatie?
VIDEO Evenzo vragen mensen: hoe beschrijf je een transformatie in wiskunde? Er zijn vier hoofdtypen van transformaties : translatie, rotatie, reflectie en dilatatie. Deze transformaties vallen in twee categorieën: rigide transformaties die de vorm of grootte van de voorafbeelding niet veranderen en niet-rigide transformaties die de grootte maar niet de vorm van de voorafbeelding wijzigen.