Video: Wat zijn puntenlijnen en vlakken?
2024 Auteur: Miles Stephen | [email protected]. Laatst gewijzigd: 2023-12-15 23:39
EEN punt in geometrie is een locatie. Het heeft geen maat, d.w.z. geen breedte, geen lengte en geen diepte. EEN punt wordt weergegeven door een punt. EEN lijn wordt gedefinieerd als a lijn van punten die zich oneindig in twee richtingen uitstrekt. EEN vlak wordt genoemd door drie punten in de vlak die niet op hetzelfde lijn.
Waarom zijn daarom puntlijnen en vlakken ongedefinieerde termen?
In Geometrie definiëren we a punt als locatie en geen maat. EEN lijn wordt gedefinieerd als iets dat zich oneindig in beide richtingen uitstrekt maar geen breedte heeft en eendimensionaal is terwijl a vlak strekt zich oneindig uit in twee dimensies. Er zijn er drie ongedefinieerde termen op het gebied van geometrie. EEN punt heeft geen maat; het heeft alleen een locatie.
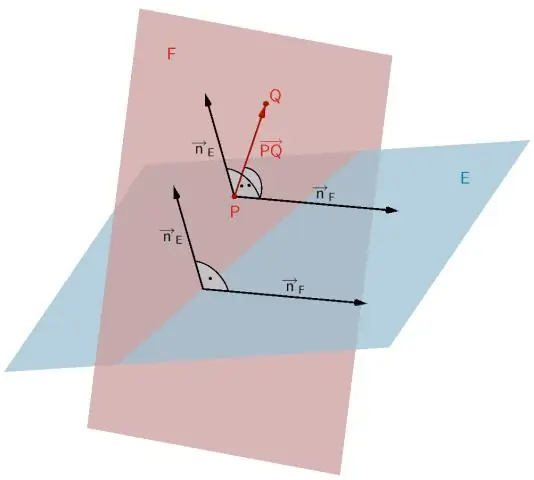
Bovendien, hoeveel vlakken bevatten elke lijn en elk punt? Als de drie punten in je diagram bijvoorbeeld A, B en C zijn, dan zijn er oneindig veel vlakken die de punten bevatten. ik heb geïllustreerd twee dergelijke vlakken in het roze in de onderstaande diagrammen. Het laatste punt is dat als de drie punten niet op een lijn liggen, er precies is één vliegtuig die de punten bevat.
Vervolgens is de vraag: wat zijn enkele voorbeelden van puntlijnen en vlakken in de echte wereld?
Voorbeelden kunnen driehoeken, vierkanten, rechthoeken, lijnen , cirkels, punten , vijfhoeken, stoptekens (achthoeken), dozen (prisma's of dobbelstenen (kubussen). Voorbeelden van een vlak zou zijn: een desktop, het krijtbord/whiteboard, een stuk papier, een tv-scherm, raam, muur of een deur.
Hoeveel punten heb je nodig om een vliegtuig te maken?
In een Euclidische ruimte van een willekeurig aantal afmetingen, wordt een vlak uniek bepaald door een van de volgende: Drie niet-collineaire punten (punten die niet op een enkele lijn liggen). Een lijn en een punt niet op die lijn. Twee duidelijke maar kruisende lijnen.
Aanbevolen:
Welke vorm hebben de 8 vlakken van een octaëder?
In de meetkunde is een octaëder (meervoud: octaëder) een veelvlak met acht vlakken, twaalf randen en zes hoekpunten. De term wordt meestal gebruikt om te verwijzen naar de regelmatige octaëder, een platonische vaste stof bestaande uit acht gelijkzijdige driehoeken, waarvan er vier samenkomen op elk hoekpunt
Wat zijn de reagentia die nodig zijn voor PCR en wat is de functie van elk?
Er zijn vijf basisreagentia of ingrediënten die bij PCR worden gebruikt: matrijs-DNA, PCR-primers, nucleotiden, PCR-buffer en Taq-polymerase. Primers worden meestal in paren gebruikt en het DNA tussen de twee primers wordt geamplificeerd tijdens de PCR-reactie
Hoeveel platte vlakken heeft de kegel?
Een plat oppervlak
Kunnen twee verschillende vlakken elkaar in een punt snijden?
Twee verschillende punten bepalen precies één lijn. Het is deze eigenschap die het vliegtuig 'plat' maakt. Twee verschillende lijnen snijden elkaar in hoogstens één punt; twee verschillende vlakken snijden elkaar in hoogstens één lijn. Als twee coplanaire lijnen elkaar niet snijden, zijn ze evenwijdig
Hoeveel randen heeft een veelvlak met vier vlakken en vier hoekpunten?
Als het vaste lichaam een veelvlak is, noem het dan en vind het aantal vlakken, randen en hoekpunten dat het heeft. De basis is een driehoek en alle zijden zijn driehoeken, dus dit is een driehoekige piramide, die ook wel een tetraëder wordt genoemd. Er zijn 4 vlakken, 6 randen en 4 hoekpunten