Inhoudsopgave:
Video: Hoe vind je de tegenovergestelde zijde van een driehoek met behulp van Pythagoras?
2024 Auteur: Miles Stephen | [email protected]. Laatst gewijzigd: 2023-12-15 23:39
Rechte driehoeken en de stelling van Pythagoras
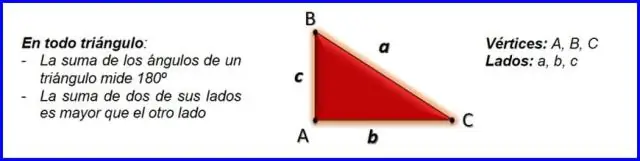
- De Pythagoras Stelling, a2+b2=c2, a 2 + b 2 = c 2, kan worden gebruikt om de lengte van elke kant van een recht driehoek .
- De kant tegenover de rechte hoek heet de hypotenusa ( kant c in de afbeelding).
Hierin, hoe vind je de tegenoverliggende zijde van een driehoek?
Om erachter te komen welke, geven we eerst namen aan de zijkanten:
- Aangrenzend grenst aan (naast) de hoek,
- Tegenover is tegenover de hoek,
- en de langste zijde is de hypotenusa.
Evenzo, wat is een formule van driehoek? De Driehoek formule worden hieronder gegeven als, Omtrek van a driehoek = a + b + c. Gebied; van; een; driehoek = frac{1}{2}bh. Waar, b is de basis van de driehoek . h is de hoogte van de driehoek.
Op dezelfde manier kan men zich afvragen, hoe vind je de ontbrekende zijde van een driehoek met één zijde en één hoek?
Stelling van Pythagoras (de stelling van Pythagoras) De hypotenusa is de langste kant van een recht driehoek , en bevindt zich tegenover de rechterkant hoek . Dus, als je de lengtes van twee kent zijkanten , het enige wat je hoeft te doen is de twee lengtes kwadrateren, het resultaat optellen en dan de vierkantswortel van de som nemen om de lengte van de hypotenusa te krijgen.
Hoe vind je de ontbrekende zijde van een gelijkbenige driehoek?
Tot vind een onbekende kant van een driehoek , je moet de lengte van de andere twee weten zijkanten en/of de hoogte. Tot vind de onbekende basis van an gelijkbenige driehoek , met behulp van het volgende: formule : 2 * sqrt(L^2 - A^2), waarbij L de lengte is van de andere twee benen en A de hoogte van de driehoek.
Aanbevolen:
Wat is het tegenovergestelde van het tegenovergestelde van - 12?
Het tegenovergestelde van 12 is 12, of een tegoed van $ 12
Hoe vind je volume met behulp van de wet van Avogadro?
De wet van Avogadro laat zien dat er een directe relatie is tussen het aantal mol van een gas en het volume ervan. Dit kan ook worden aangetoond met behulp van de vergelijking: V1/n1 = V2/n2. Als het aantal mol wordt verdubbeld, verdubbelt het volume
Hoe vind je de oppervlakte van een piramide met behulp van een net?
VIDEO Wat is hierbij de totale oppervlakte van een piramide? De Oppervlakte van een piramide Als alle zijvlakken hetzelfde zijn: [Base Gebied ] + 1 / 2 × Omtrek × [Slantlengte] Je kunt je ook afvragen, hoe vind je het oppervlak van een bol?
Wat is de flux door een kubus van zijde als een puntlading van Q zich in een van zijn hoeken bevindt?
Zoals we dat weten, is de totale flux van een lading q q/ε0 (wet van Gauss). Als de lading zich op de hoek van een kubus bevindt, komt een deel van de flux de kubus binnen en verlaat deze via enkele van zijn vlakken. Maar een deel van de flux komt niet in de kubus. Deze 1/8e wordt weer opgedeeld in 3 delen
Hoe vind je het gebied van het gezicht met behulp van het oppervlak?
Oppervlakte is de som van de gebieden van alle vlakken (of oppervlakken) op een 3D-vorm. Een balk heeft 6 rechthoekige vlakken. Om de oppervlakte van een balk te vinden, telt u de oppervlakten van alle 6 vlakken op. We kunnen ook de lengte (l), breedte (w) en hoogte (h) van het prisma benoemen en de formule SA=2lw+2lh+2hw gebruiken om de oppervlakte te vinden