Video: Hoe vind je het gebied van het gezicht met behulp van het oppervlak?
2024 Auteur: Miles Stephen | [email protected]. Laatst gewijzigd: 2023-12-15 23:39
Oppervlakte is de som van de gebieden van alles gezichten (of oppervlakken) op een 3D-vorm. Een balk heeft 6 rechthoekige gezichten . om de te vinden oppervlakte van een balk, voeg de toe gebieden van alle 6 gezichten . We kunnen ook de lengte (l), breedte (w) en hoogte (h) van het prisma labelen en gebruik maken van de formule, SA=2lw+2lh+2hw, om de. te vinden oppervlakte.
Dus, hoe vind je het gebied van een gezicht?
Juiste antwoord: De Oppervlakte van elke gezicht wordt gevonden door de lengte van de zijde te kwadrateren. Vermenigvuldig de Oppervlakte van een gezicht door het aantal gezichten om het totale oppervlak te krijgen Oppervlakte van de kubus.
Evenzo, wat is de oppervlakte van de bol? EEN gebied met straal r heeft een volume van 4 3 π r 3 frac{4}{3} pi r^3 34πr3 en een oppervlak Oppervlakte van 4 π r 2 4 pi r^2 4πr2. EEN gebied heeft verschillende interessante eigenschappen, waaronder die van alle vormen met hetzelfde oppervlak Oppervlakte , de gebied heeft het grootste volume.
Zo ja, wat is de formule voor het vinden van de oppervlakte van een rechthoekig prisma?
De formule om de oppervlakte van een rechthoekig prisma te vinden is A = 2wl + 2lh + 2hw, waarbij w de breedte is, de l de lengte en de h de hoogte.
Wat is de formule voor het vinden van de oppervlakte van een kubus?
Vinden het oppervlak oppervlakte van een kubus , gebruik de formule : oppervlakte Oppervlakte = 6s^2, waarbij s de lengte is van een van de zijden. Als je de lengte van de zijkanten niet weet, kun je het oppervlak vinden Oppervlakte volume gebruiken. Vind gewoon de kubus wortel van het volume, die gelijk is aan de lengte van één zijde van de kubus.
Aanbevolen:
Hoe vind je het geschatte percentage met behulp van de empirische regel?
Het gebied onder de curve vinden van x = 9 tot x = 13. De empirische regel of 68-95-99,7% regel geeft het geschatte percentage gegevens dat binnen één standaarddeviatie (68%), twee standaarddeviaties (95%) valt. , en drie standaarddeviaties (99,7%) van het gemiddelde
Hoe vind je de tegenovergestelde zijde van een driehoek met behulp van Pythagoras?
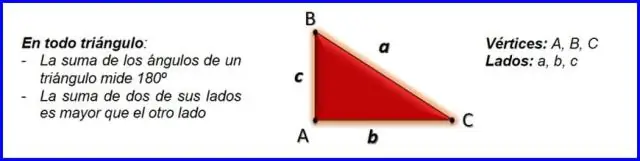
Rechte driehoeken en de stelling van Pythagoras De stelling van Pythagoras, a2+b2=c2, a 2 + b 2 = c 2, kan worden gebruikt om de lengte van elke zijde van een rechthoekige driehoek te bepalen. De zijde tegenover de rechte hoek wordt de hypotenusa genoemd (zijde c in de figuur)
Hoe vind je volume met behulp van de wet van Avogadro?
De wet van Avogadro laat zien dat er een directe relatie is tussen het aantal mol van een gas en het volume ervan. Dit kan ook worden aangetoond met behulp van de vergelijking: V1/n1 = V2/n2. Als het aantal mol wordt verdubbeld, verdubbelt het volume
Hoe vind je de oppervlakte van een piramide met behulp van een net?
VIDEO Wat is hierbij de totale oppervlakte van een piramide? De Oppervlakte van een piramide Als alle zijvlakken hetzelfde zijn: [Base Gebied ] + 1 / 2 × Omtrek × [Slantlengte] Je kunt je ook afvragen, hoe vind je het oppervlak van een bol?
Hoe vind je een gebied met zonde?
Het gebied van een driehoek vinden met behulp van sinus. U bent bekend met de formule R=12bh om de oppervlakte van een driehoek te vinden waarbij b de lengte is van een basis van de driehoek en h de hoogte is, of de lengte van de loodlijn op de basis vanaf het tegenoverliggende hoekpunt. Stel dat ΔABC de lengtes a, b en c . heeft