Inhoudsopgave:
Video: Hoe los je de optellingseigenschap van gelijkheid op?
2024 Auteur: Miles Stephen | [email protected]. Laatst gewijzigd: 2023-12-15 23:39
Toevoeging eigendom van gelijkheid
Als twee uitdrukkingen aan elkaar gelijk zijn en u dezelfde waarde aan beide zijden van de vergelijking toevoegt, blijft de vergelijking gelijk. Wanneer je oplossen een vergelijking, vind je de waarde van de variabele die de vergelijking waar maakt. Om zo te oplossen de vergelijking, isoleert u de variabele.
Dienovereenkomstig, wat betekent de toevoegingseigenschap van gelijkheid?
Toevoeging eigendom van gelijkheid . De eigendom die stelt dat als u hetzelfde getal aan beide zijden van een vergelijking toevoegt, de zijden gelijk blijven (d.w.z. de vergelijking blijft waar.)
Bovendien, welke uitspraak is een voorbeeld van de toevoegingseigenschap van gelijkheid? De additieve eigenschap van gelijkheid stelt dat als hetzelfde bedrag aan beide zijden van een vergelijking wordt toegevoegd, de gelijkwaardigheid is nog steeds waar. Laat a, b en c reële getallen zijn, die bestaan uit rationale getallen (bijv. 0, -7 en 2/3) en irrationele getallen (bijv. pi en de vierkantswortel van 5).
Evenzo wordt gevraagd: hoe los je gelijkheden op?
Samenvatting
- Veel eenvoudige ongelijkheden kunnen worden opgelost door beide zijden op te tellen, af te trekken, te vermenigvuldigen of te delen totdat u de variabele alleen overhoudt.
- Maar deze dingen zullen de richting van de ongelijkheid veranderen:
- Vermenigvuldig of deel niet door een variabele (tenzij u weet dat deze altijd positief of altijd negatief is)
Wat zijn de 4 eigenschappen van gelijkheid?
- De reflexieve eigenschap. een = een.
- De symmetrische eigenschap. Als a=b, dan is b=a.
- De transitieve eigenschap. Als a=b en b=c, dan is a=c.
- De vervangingseigenschap. Als a = b, dan kan a in elke vergelijking worden vervangen door b.
- De eigenschappen van optellen en aftrekken.
- De vermenigvuldigingseigenschappen.
- De Divisie Eigenschappen.
- The Square Roots-eigenschap *
Aanbevolen:
Hoe verschilt de vorm van een plantencel van die van een dierlijke cel?
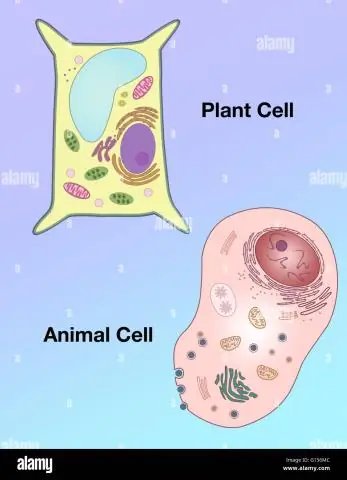
Vacuolen: Plantencellen hebben een grote vacuole, terwijl dierlijke cellen meerdere kleine vacuolen bevatten. Vorm: Plantencellen hebben een meer regelmatige vorm (meestal rechthoekig), terwijl dierlijke cellen onregelmatige vormen hebben. Lysosomen: zijn over het algemeen aanwezig in dierlijke cellen, terwijl ze afwezig zijn in plantencellen
Wat betekent vermenigvuldigingseigenschap van gelijkheid?
Vermenigvuldigingseigenschap van gelijkheid. De vermenigvuldigingseigenschap van gelijkheid stelt dat als je beide zijden van een vergelijking met hetzelfde getal vermenigvuldigt, de zijden gelijk blijven (d.w.z. de gelijkheid blijft behouden)
Wat is de eigenschap van gelijkheid in wiskunde?
Eigenschappen van gelijkheden. Twee vergelijkingen die dezelfde oplossing hebben, worden equivalente vergelijkingen genoemd, b.v. 5 +3 = 2 + 6. En dit, zoals we in een vorige paragraaf hebben geleerd, wordt weergegeven door het gelijkheidsteken =. Een inverse operatie zijn twee operaties die elkaar ongedaan maken, b.v. optellen en aftrekken of vermenigvuldigen en delen
Hoe is de wet van behoud van energie van toepassing op energietransformaties?
De wet van behoud van energie stelt dat energie niet kan worden gecreëerd of vernietigd - alleen omgezet van de ene vorm van energie in de andere. Dit betekent dat een systeem altijd dezelfde hoeveelheid energie heeft, tenzij het van buitenaf wordt toegevoegd. De enige manier om energie te gebruiken is om energie van de ene vorm naar de andere te transformeren
Hoe los je problemen met de massa van de massa van de reactanten op?
Vind het beperkende reagens door de hoeveelheid product te berekenen en te vergelijken die elke reactant zal produceren. Breng de chemische vergelijking voor de chemische reactie in evenwicht. Zet de gegeven informatie om in mollen. Gebruik stoichiometrie voor elke afzonderlijke reactant om de geproduceerde massa van het product te vinden