Video: Hoe kan het coördinatenvlak je helpen bepalen dat de corresponderende zijden congruent zijn?
2024 Auteur: Miles Stephen | [email protected]. Laatst gewijzigd: 2023-12-15 23:39
Gegeven twee driehoeken op a coördinaatvlak , jij kan controleer of ze zijn congruent met behulp van de afstandsformule tot vind de lengte van hun zijkanten . Als drie paar zijden zijn congruent , dan zijn de driehoeken congruent door de bovenstaande stelling.
Dienovereenkomstig, hoe bepaal je of twee punten congruent zijn?
Twee driehoeken zijn congruent als ze hebben: precies dezelfde drie kanten en. precies dezelfde drie hoeken.
Er zijn vijf manieren om te bepalen of twee driehoeken congruent zijn: SSS, SAS, ASA, AAS en HL.
- SSS (zijkant, zijkant, zijkant)
- SAS (zijde, hoek, zijde)
- ASA (hoek, zijde, hoek)
- AAS (hoek, hoek, zijde)
- HL (hypotenusa, been)
Vervolgens is de vraag, wat betekent het dat Angle congruent is? Congruente hoeken heb hetzelfde hoek (in graden of radialen). Dat is alle. Deze hoeken zijn congruent . Ze hoeven niet in dezelfde richting te wijzen. Ze hoeven niet op lijnen van vergelijkbare grootte te staan.
Trouwens, wat is een congruentieverklaring?
EEN congruentieverklaring is een uitspraak gebruikt in de geometrie die simpelweg zegt dat twee objecten zijn congruent , of exact dezelfde vorm en grootte hebben.
Zijn evenwijdige lijnen congruent?
Als twee parallelle lijnen worden gesneden door een transversaal, de bijbehorende hoeken zijn congruent . Als twee lijnen worden gesneden door een transversaal en de bijbehorende hoeken zijn congruent , de lijnen zijn evenwijdig . Binnenhoeken aan dezelfde zijde van de transversale: De naam is een beschrijving van de "locatie" van deze hoeken.
Aanbevolen:
Wat betekent het dat segmenten congruent zijn?
Congruente segmenten zijn eenvoudig lijnsegmenten die even lang zijn. Congruent betekent gelijk. Congruente lijnsegmenten worden meestal aangegeven door hetzelfde aantal tic-lijntjes in het midden van de segmenten te tekenen, loodrecht op de segmenten. We geven een lijnsegment aan door een lijn over zijn twee eindpunten te tekenen
Hoe kan waterstofbinding tussen watermoleculen helpen bij het verklaren van het vermogen van water om grote hoeveelheden energie te absorberen voordat het verdampt?
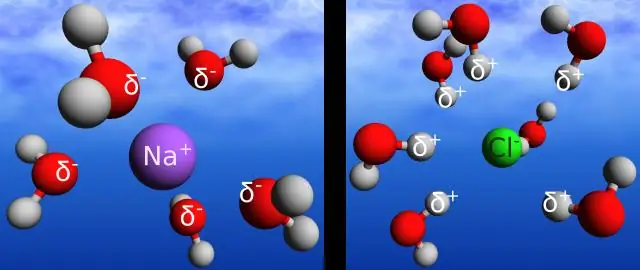
Door de waterstofbruggen in water kan het warmte-energie langzamer absorberen en afgeven dan veel andere stoffen. Temperatuur is een maat voor de beweging (kinetische energie) van moleculen. Naarmate de beweging toeneemt, is de energie hoger en dus de temperatuur hoger
Hoe kan een model helpen bij het vinden van de waarschijnlijkheid van een samengestelde gebeurtenis?
Definitie van waarschijnlijkheid van samengestelde gebeurtenissen Een samengestelde gebeurtenis is een gebeurtenis waarbij er meer dan één mogelijke uitkomst is. Het bepalen van de waarschijnlijkheid van een samengestelde gebeurtenis omvat het vinden van de som van de kansen van de afzonderlijke gebeurtenissen en, indien nodig, het verwijderen van overlappende kansen
Hoe bewijs je dat twee segmenten congruent zijn?
Congruente segmenten zijn eenvoudig lijnsegmenten die even lang zijn. Congruent betekent gelijk. Congruente lijnsegmenten worden meestal aangegeven door hetzelfde aantal ticlijnen in het midden van de segmenten, loodrecht op de segmenten, te tekenen. We geven een lijnstuk aan door een lijn over zijn twee eindpunten te tekenen
Hoe werkt het Aufbau-principe, dat is wat het betekent om te zeggen dat orbitalen van onder naar boven of van boven naar beneden worden gevuld, afhankelijk van het diagram)?
Van beneden naar boven: Kamers moeten vanaf de begane grond worden gevuld. Op hogere verdiepingen kan de volgorde een beetje veranderen. Aufbau-principe: de elektronen vullen de beschikbare orbitalen van de laagste energie tot de hoogste energie. In de grondtoestand bevinden alle elektronen zich in het laagst mogelijke energieniveau