Video: Hoe doe je de uitbreiding van de vermogensreeks?
2024 Auteur: Miles Stephen | [email protected]. Laatst gewijzigd: 2023-12-15 23:39
Uitbreidingen Power Series . Rn=f(n+1)(ξ)(x−a)n+1(n+1)!, a<ξ<x. Als dit uitbreiding convergeert over een bepaald bereik van x gecentreerd op a, dat wil zeggen, limn→∞Rn=0, dan is de uitbreiding wordt genoemd Taylor-serie van de functie f(x) geëxpandeerd rond het punt a.
Wat is in dit verband de som van een machtreeks?
(x-a)n. Of de serie convergeert of divergeert, en de waarde waar het naar toe convergeert, hangt af van de gekozen x-waarde, waardoor kracht series een functie.
Bovendien, waar worden Power-series voor gebruikt? Kracht series uitbreidingen kunnen zijn: gebruikt om de waarden van bepaalde integralen te benaderen, en een bekend voorbeeld is de foutintegraal (integrand is e−x2) omdat dit leidt tot een alternerende serie (zelfs als x negatief is), en dus kan de fout gemakkelijk worden geschat.
Kan hierin elke functie worden weergegeven als een machtreeks?
3 antwoorden. EEN functie kan zijn weergegeven als een machtreeks dan en slechts als het complex differentieerbaar is in een open verzameling. Dit volgt uit de algemene vorm van de stelling van Taylor voor complex functies . De reden is dat de complexe versie van de functie is niet eens continu in de oorsprong.
Wat is de convergentiestraal van een machtreeks?
Straal van convergentie . Van Wikipedia, de gratis encyclopedie. In de wiskunde is de convergentiestraal van een machtreeks is de straal van de grootste schijf waarin de reeks convergeert . Het is ofwel een niet-negatief reëel getal of..
Aanbevolen:
Hoe doe je de Durbin Watson-test in Minitab?
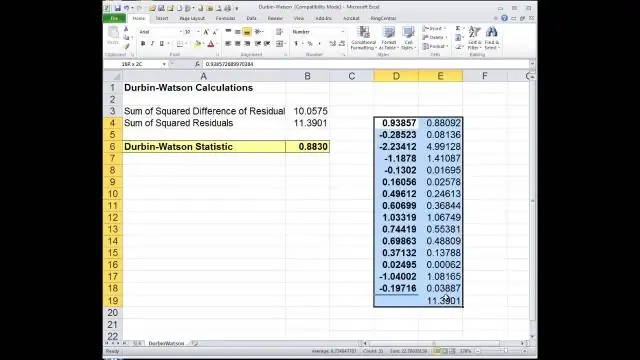
In Minitab: Klik op Statistiek > Regressie > Regressie > Regressiemodel passen. Klik op 'Resultaten' en controleer de Durbin-Watson-statistiek
Hoe doe je stelsel van vergelijkingen woordproblemen?
Om een stelsel van vergelijkingswoordproblemen op te lossen, definiëren we eerst de variabelen en extraheren we de vergelijkingen uit de woordproblemen. We kunnen het systeem dan oplossen met behulp van grafische, eliminatie- of substitutiemethoden
Hoe doe je waarschijnlijkheid samengestelde gebeurtenissen?
Het bepalen van de waarschijnlijkheid van een samengestelde gebeurtenis omvat het vinden van de som van de kansen van de afzonderlijke gebeurtenissen en, indien nodig, het verwijderen van overlappende kansen. Een exclusieve samengestelde gebeurtenis is een gebeurtenis waarin de meerdere gebeurtenissen elkaar niet overlappen. In wiskundige termen: P(C) = P(A) + P(B)
Hoe doe je een eenvoudige continuïteitstester?
VIDEO De vraag is ook, wat is een eenvoudige continuïteitstester? EEN continuïteitstester is een eenvoudig apparaat bestaande uit twee testsondes en een licht (LED) of zoemerindicator. Het wordt gebruikt om de aanwezigheid van continuïteit of een breuk tussen de twee uiteinden van een geleider die is verbonden met de testsondes.
Hoe doe je sinusoïdale regressie op een rekenmachine?
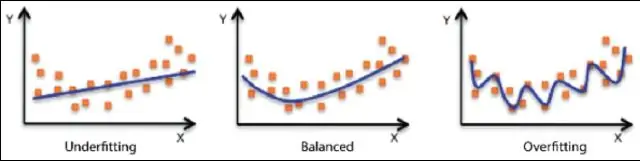
VIDEO Hiervan, hoe bereken je sinusoïdale regressie? Sinusvormige regressie . Pas de waarden van A, B, C en D aan in de vergelijking y = A*sin(B(x-C))+D om a. te maken sinusvormig curve past bij een bepaalde set willekeurig gegenereerde gegevens.