
- Auteur Miles Stephen [email protected].
- Public 2023-12-15 23:39.
- Laatst gewijzigd 2025-06-01 05:05.
Als een parabool heeft een horizontaal as, de standaardvorm van de vergelijking van de parabool is dit: (y -k)2 = 4p(x - h), waarbij p≠ 0. The hoekpunt van dit parabool is bij (h, k). De focus ligt op (h + p, k). De richtlijn is de lijn x = h - p.
Zo, hoe vind je het hoekpunt en de richtlijn van een parabool?
De standaardvorm is (x - h)2 = 4p (y - k), waarbij de focus is (h, k + p) en de richtlijn is y= k - p. Als de parabool wordt gedraaid zodat zijn hoekpunt is (h, k) en zijn symmetrieas is evenwijdig aan de x-as, hij heeft een vergelijking van (y - k)2 = 4p (x -h), waarbij de focus is (h + p, k) en de richtlijn is x = h - p.
Bovendien, wat is de vergelijking voor een zijwaartse parabool? De "algemene" vorm van a vergelijking van parabool isdegene die je gewend bent, y = ax2 + bx + c - tenzij de kwadratische is " zijwaarts ", in welk geval de vergelijking ziet er ongeveer uit als x = ay2 + door +c.
Zo, hoe vind je het hoekpunt van een paraboolvergelijking?
Dit punt, waar de parabool van richting verandert, wordt de " hoekpunt ". Als de kwadratische is geschreven in de vorm y = a(x - h)2 + k, dan de hoekpunt is het punt (h, k). Dit is logisch, als je erover nadenkt. Het kwadraatgedeelte is altijd positief (voor een rechter-side-up parabool ), tenzij het nul is.
Voor welke waarde van p heeft het hoekpunt van de parabool?
Het absolute waarde van p is de afstand tussen de hoekpunt en de focus en de afstand tussen de hoekpunt en de richtlijn. (Het aanmelden P vertelt me op welke manier de parabool gezichten.) Aangezien het brandpunt en de richtlijn twee eenheden van elkaar verwijderd zijn, moet deze afstand één eenheid zijn, dus | P | = 1.
Aanbevolen:
Is de boog van Saint Louis een parabool?

Dit artikel heeft aangetoond dat de Gateway Arch geen parabool is. Het heeft eerder de vorm van een afgeplatte (of verzwaarde) bovenleiding, wat de vorm is die we zien als we een ketting ophangen die dun is in het midden tussen twee vaste punten
Hoe vind je de vergelijking van een lijn gegeven een punt en een parallelle lijn?

De vergelijking van de lijn in de vorm van het helling-snijpunt is y=2x+5. De helling van de parallellijn is hetzelfde: m=2. De vergelijking van de parallelle lijn is dus y=2x+a. Om a te vinden, gebruiken we het feit dat de lijn door het gegeven punt moet gaan:5=(2)⋅(&min;3)+a
Hoe heet de top van een piramide?

Een piramidale piek, in extreme gevallen soms een gletsjerhoorn genoemd, is een hoekige, scherp gepunte bergtop die het gevolg is van de cirque-erosie als gevolg van meerdere gletsjers die uiteenlopen van een centraal punt. Piramidale pieken zijn vaak voorbeelden van nunataks
Hoe teken je een kegelsnede van een parabool?
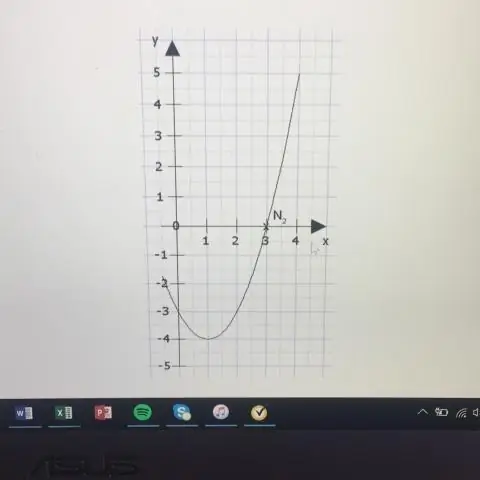
De richtlijn is de lijn y = k - p. De as is de lijn x = h. Als p > 0, opent de parabool naar boven, en als p < 0, opent de parabool naar beneden. Als een parabool een horizontale as heeft, is de standaardvorm van de vergelijking van de parabool deze: (y - k)2 = 4p(x - h), waarbij p≠ 0
Hoe maak je een kegelsnede van een parabool?
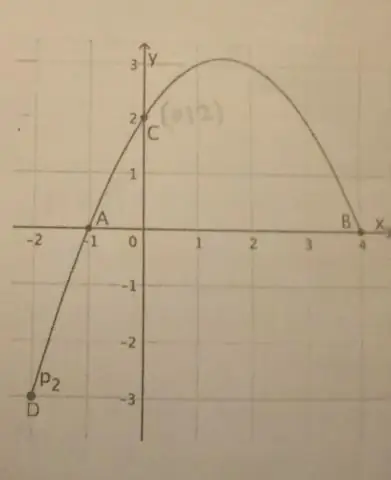
Als een parabool een verticale as heeft, is de standaardvorm van de vergelijking van de parabool deze: (x - h)2 = 4p(y - k), waarbij p≠ 0. Het hoekpunt van deze parabool is op (h, k). De focus ligt op (h, k + p). De richtlijn is de lijn y = k - p
