Video: Hoe maak je een kegelsnede van een parabool?
2024 Auteur: Miles Stephen | [email protected]. Laatst gewijzigd: 2023-12-15 23:39
Als een parabool heeft een verticale as, de standaardvorm van de vergelijking van de parabool is dit: (x - h)2 = 4p(y - k), waarbij p≠ 0. Het hoekpunt hiervan parabool is bij (h, k). De focus ligt op (h, k + p). De richtlijn is de lijn y = k - p.
Mensen vragen zich ook af: is een parabool een kegelsnede?
De parabool is een ander algemeen bekend kegelsnede . De geometrische definitie van a parabool is de meetkundige plaats van alle punten zodat ze op gelijke afstand van een punt, bekend als het brandpunt, en een rechte lijn, de richtlijn genoemd, zijn. Met andere woorden de excentriciteit van a parabool gelijk is aan 1.
Bovendien, wat zijn de 4 soorten kegelsneden? De vier kegelsneden zijn: cirkels , ellipsen, parabolen en hyperbolen. Kegelsneden zijn al geruime tijd bestudeerd. Kepler merkte voor het eerst op dat planeten elliptische banen hadden. Afhankelijk van de energie van een in een baan om de aarde draaiend lichaam, zijn baanvormen mogelijk die elk van de vier soorten kegelsneden zijn.
Evenzo, hoe maak je een kegelsnede?
kegelsneden worden gegenereerd door het snijpunt van een vlak met een kegel. Als het vlak evenwijdig is aan de omwentelingsas (de y -as), dan is de kegelsnede is een hyperbool. Als het vlak evenwijdig is aan de genererende lijn, is de kegelsnede is een parabool.
Wat is de standaardvorm van een parabool?
f (x) = a(x - h)2 + k, waarbij (h, k) het hoekpunt is van de parabool . Ter info: verschillende leerboeken hebben verschillende interpretaties van de referentie " standaard vorm " van een kwadratische functie. Sommigen zeggen f (x) = ax2 + bx + c is " standaard vorm ", terwijl anderen zeggen dat f (x) = a(x - h)2 + k is " standaard vorm ".
Aanbevolen:
Hoe maak je een kopie van een hoek met een kompas?
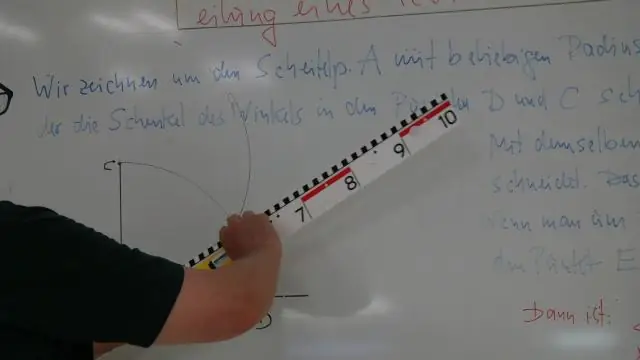
Een hoek kopiëren met een kompas Teken een werklijn, l, met punt B erop. Open je kompas naar elke straal r, en constructieboog (A, r) die de twee zijden van hoek A snijdt in de punten Zand T. Construeer boog (B, r) die lijn l snijdt op een punt V. Construeer boog (S, ST). Construeer boog (V, ST) kruisende boog (B, r) op punt W
Hoe teken je een kegelsnede van een parabool?
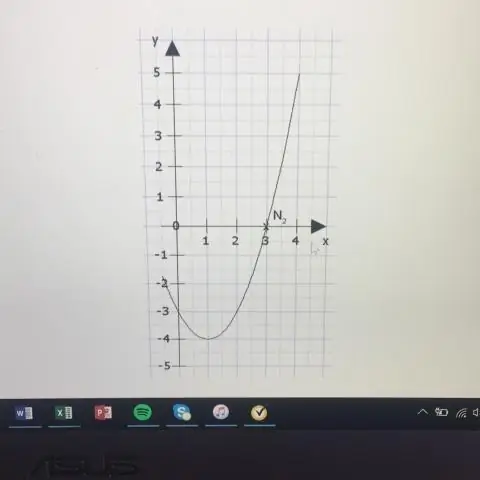
De richtlijn is de lijn y = k - p. De as is de lijn x = h. Als p > 0, opent de parabool naar boven, en als p < 0, opent de parabool naar beneden. Als een parabool een horizontale as heeft, is de standaardvorm van de vergelijking van de parabool deze: (y - k)2 = 4p(x - h), waarbij p≠ 0
Hoe vind je de top van een horizontale parabool?
Als een parabool een horizontale as heeft, is de standaardvorm van de vergelijking van de parabool deze: (y -k)2 = 4p(x - h), waarbij p≠ 0. Het hoekpunt van deze parabool is op (h, k). De focus ligt op (h + p, k). De richtlijn is de lijn x = h - p
Is cirkel een kegelsnede?
Een kegelsnede is in feite de figuur die tevoorschijn komt uit de kruising tussen een kegel en een vlak. Cirkel wordt beschouwd als een speciaal type ellips, en dus een kegelsnede. Een snijpunt tussen een rechte cirkelvormige kegel met een vlak in een rechte hoek zou een cirkel produceren, en daarom is een cirkel ook een kegelsnede
Hoe vind je het middelpunt van een cirkel in een kegelsnede?
De waarde van r wordt de 'straal' van de cirkel genoemd en het punt (h, k) wordt het 'middelpunt' van de cirkel genoemd. (h, k) = (0, 0), dan vereenvoudigt de vergelijking tot x2 + y2 = r2