Video: Wat is een Biconditional-statement in de logica?
2024 Auteur: Miles Stephen | [email protected]. Laatst gewijzigd: 2023-12-15 23:39
Wanneer we twee voorwaardelijke combineren uitspraken op deze manier hebben we een biconditioneel . Definitie: A bivoorwaardelijke verklaring wordt gedefinieerd als waar wanneer beide delen dezelfde waarheidswaarde hebben. De biconditioneel p q staat voor "p als en slechts als q", waarbij p een hypothese is en q een conclusie.
Evenzo, wanneer kunt u een Biconditional-verklaring schrijven?
' Biconditionele uitspraken zijn waar uitspraken die de hypothese en de conclusie combineren met de sleutelwoorden 'als en slechts als'. 'Bijvoorbeeld de verklaring zal deze vorm aannemen: (hypothese) als en slechts als (conclusie). We konden ook schrijven het op deze manier: (conclusie) als en slechts als (hypothese).
Wat betekent IFF naast het bovenstaande wanneer het wordt gebruikt in een Biconditional-statement? In logica en aanverwante gebieden zoals wiskunde en filosofie, als en slechts als (afgekort als iff ) is een biconditioneel logisch verband tussen uitspraken , waar ofwel beide uitspraken zijn waar of beide zijn vals.
Weet ook, wat is de ontkenning van een Bivoorwaardelijke verklaring?
De negatie hiervan is wanneer de ene waar is en de andere onwaar, en dat is precies wat je hebt geschreven. Dat gezegd hebbende, zou het er niet echt toe moeten doen, omdat je niet zowel p∧∼q als ∼p∧q kunt hebben, want dat zou betekenen dat je p∧∼p (en q∧∼q) hebt, wat nooit kan.
Wat is een voorbeeld van een Biconditional statement?
Voorbeelden van bivoorwaardelijke verklaringen De bivoorwaardelijke uitspraken voor deze twee verzamelingen zou zijn: De veelhoek heeft slechts vier zijden dan en slechts dan als de veelhoek een vierhoek is. De veelhoek is een vierhoek dan en slechts dan als de veelhoek maar vier zijden heeft.
Aanbevolen:
Wat is het verschil tussen een ultramafische, een mafic, een intermediate en een felsic rock?
In een algemeen aanvaard classificatieschema voor silica-inhoud worden gesteenten met meer dan 65 procent silica felsisch genoemd; die met tussen 55 en 65 procent silica zijn intermediair; die met tussen de 45 en 55 procent silica zijn mafic; en degenen met minder dan 45 procent zijn ultramafisch
Hoe schrijf je een Biconditional als twee conditionals?
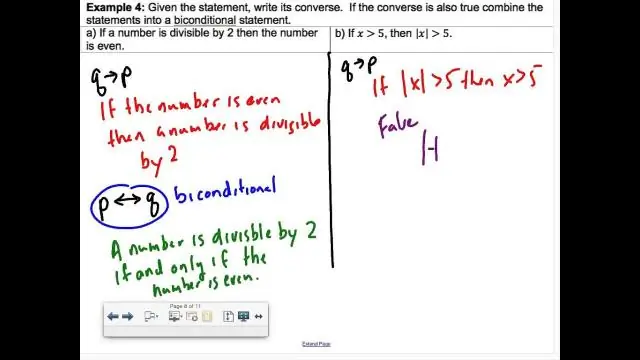
Het is een combinatie van twee voorwaardelijke uitspraken, "als twee lijnsegmenten congruent zijn, zijn ze even lang" en "als twee lijnsegmenten even lang zijn, zijn ze congruent". Een biconditional is waar als en slechts als beide conditionals waar zijn. Bi-conditionals worden weergegeven door het symbool ↔ of ⇔
Wat maakt een zuur tot een zuur en een base tot een base?
Een zuur is een stof die waterstofionen afstaat. Hierdoor wordt, wanneer een zuur wordt opgelost in water, de balans tussen waterstofionen en hydroxide-ionen verschoven. Dit soort oplossing is zuur. Een base is een stof die waterstofionen accepteert
Wat is een structuurformule Wat is het verschil tussen een structuurformule en een moleculair model?
Een molecuulformule gebruikt chemische symbolen en subscripts om het exacte aantal verschillende atomen in een molecuul of verbinding aan te geven. Een empirische formule geeft de eenvoudigste, gehele getalsverhouding van atomen in een verbinding. Een structuurformule geeft de bindingsrangschikking van de atomen in het molecuul aan
Wat is de logica die ten grondslag ligt aan de theorie van spontane generatie?
De theorie van spontane generatie hield in dat levende wezens konden ontstaan uit niet-levende materie en dat dergelijke processen alledaags en regelmatig waren. Er werd bijvoorbeeld verondersteld dat bepaalde vormen zoals vlooien zouden kunnen ontstaan uit levenloze materie zoals stof, of dat maden zouden kunnen ontstaan uit dood vlees