Inhoudsopgave:
Video: Wat is rechtvaardiging in de algebra?
2024 Auteur: Miles Stephen | [email protected]. Laatst gewijzigd: 2023-12-15 23:39
Rechtvaardiging : Toevoegingseigenschap van gelijkheid (De hoeveelheid x is toegevoegd aan elke kant van de vergelijking.) Rechtvaardiging : Aftrekkingseigenschap van gelijkheid (Er werden twee afgetrokken van elke kant van de vergelijking.) Rechtvaardiging : Delingseigenschap van gelijkheid (Elke zijde van de vergelijking werd gedeeld door vier.)
Bovendien, wat is een rechtvaardiging in wiskunde?
Naar mij, " verantwoorden " betekent het neerleggen van de wiskundig denkproces stap voor stap, zodat de lijn van het beginpunt naar het eindpunt is verbonden. Het is iets minder formeel dan een bewijs, dat bepaalde logische vereisten heeft, maar het betekent: "laat genoeg werk zien zodat ik weet dat je het hele ding krijgt."
Evenzo, wat is een voorbeeld van rechtvaardiging? zelfstandig naamwoord. De definitie van rechtvaardiging is iets dat bewijst, verklaart of ondersteunt. Een voorbeeld van rechtvaardiging is een werkgever die bewijs levert om te ondersteunen waarom hij een werknemer heeft ontslagen. YourDictionary-definitie en gebruik voorbeeld.
Wat betekent het in dit verband om uw antwoord te rechtvaardigen?
werkwoord. De definitie van verantwoorden is het geven van een verklaring of reden voor iets om het in orde te laten lijken of om te bewijzen dat het juist of in orde is. Een voorbeeld van verantwoorden is wanneer u gegevens verstrekt ter ondersteuning van een aanbeveling die u doet. Een voorbeeld van verantwoorden is wanneer je een excuus verzint om slecht gedrag goed te laten lijken.
Wat zijn de eigenschappen van vergelijkingen in wiskunde?
Eigenschappen van vergelijkingen:
- Toevoegingseigenschap van gelijkheid: Als A = B, dan is A + C = B + C.
- Vermenigvuldigingseigenschap van gelijkheid: A = B, dan AC = BC.
- Delingseigenschap van gelijkheid: Als A = B, dan is A/C = B/C waarbij C≠0.
- Absolute waardevergelijkingseigenschap: Als |A| = B, dan zijn A = B en -A = B beide mogelijke oplossingen.
Aanbevolen:
Wat is een groep in de algebra?
In de wiskunde is een groep een verzameling die is uitgerust met een binaire bewerking die twee elementen combineert om een derde element te vormen op een zodanige manier dat wordt voldaan aan vier voorwaarden die groepsaxioma's worden genoemd, namelijk sluiting, associativiteit, identiteit en invertibiliteit. Groepen delen een fundamentele verwantschap met het begrip symmetrie
Wat is een identiteit in Algebra 2?
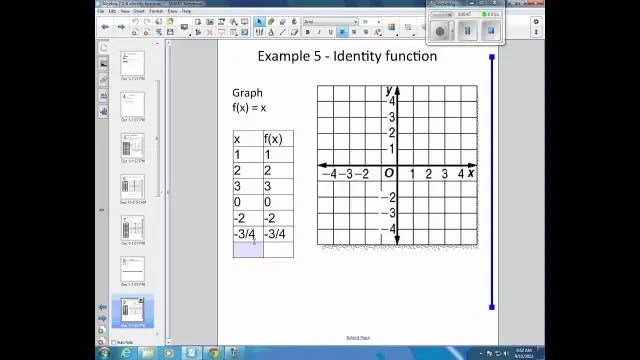
Een identiteitsvergelijking is een vergelijking die altijd geldt voor elke waarde die in de variabele is gesubstitueerd. Bijvoorbeeld, 2 (x + 1) = 2 x + 2 2(x+1)=2x+2 2(x+1)=2x+2 is een identiteitsvergelijking
Wat is de taal van algebra?
Algebra leren lijkt een beetje op het leren van een andere taal. In feite is algebra een eenvoudige taal die wordt gebruikt om wiskundige modellen van situaties uit de echte wereld te maken en om problemen aan te pakken die we niet alleen met rekenen kunnen oplossen. In plaats van woorden te gebruiken, gebruikt algebra symbolen om uitspraken over dingen te doen
Wat is het verschil tussen Algebra 1 en Algebra 2?
De primaire focus van Algebra 1 is het oplossen van vergelijkingen. De enige functies die u uitgebreid zult bekijken, zijn lineair en kwadratisch. Algebra 2 is veel geavanceerder
Is intermediaire algebra Algebra 2?
Dit leerboek voor Intermediate Algebra is ontworpen als een chronologische cursus om u te begeleiden bij High School Algebra (soms op sommige locaties Algebra II genoemd). Dit leerboek gaat ervan uit dat je Rekenkunde en Algebra hebt voltooid. Hoewel niet vereist, wordt Intermediate Algebra normaal gesproken het jaar na Geometry genomen