Inhoudsopgave:
Video: Hoe gebruik je synthetische deling om het quotiënt te vinden?
2024 Auteur: Miles Stephen | [email protected]. Laatst gewijzigd: 2023-12-15 23:39
VIDEO
Als u dit in overweging neemt, hoe vindt u het delerdividend en het quotiënt met behulp van synthetische deling?
Synthetische deling door x − a
- 47 = 9· 5 + 2.
- Dividend = Quotiënt· Deler + Rest.
- P(x) = Q(x)· D(x) + R(x).
- Haal de leidende coëfficiënt (1) naar beneden, vermenigvuldig deze met a (2), en. schrijf dat product (1· 2) in de tweede kolom:
- Herhaal het proces. −3· 2 = −6.
- Oplossing.
- P(x) = Q(x)· D(x) + R.
Evenzo, hoe los je een synthetisch delingsprobleem op? Synthetische deling is een andere manier om een polynoom te delen door de binomiale x - c, waarbij c een constante is.
- Stap 1: Zet de synthetische afdeling op.
- Stap 2: Breng de leidende coëfficiënt naar de onderste rij.
- Stap 3: Vermenigvuldig c met de waarde die zojuist op de onderste rij is geschreven.
- Stap 4: Voeg de kolom toe die in stap 3 is gemaakt.
Ook om te weten, wat is een synthetische delingsmethode?
synthetische divisie is een afkorting, of snelkoppeling, methode van polynomiale deling in het speciale geval van delen door een lineaire factor -- en het werkt alleen in dit geval. synthetische divisie wordt echter over het algemeen niet gebruikt om factoren uit te splitsen, maar om nullen (of wortels) van veeltermen te vinden. Hierover later meer.
Wat is synthetische deling en voorbeelden?
synthetische divisie is een verkorte methode voor het delen van veeltermen voor het speciale geval van delen door een lineaire factor waarvan de leidende coëfficiënt 1 is. Om het proces te illustreren, herinnert u zich de voorbeeld aan het begin van de sectie. Deel 2x3−3x2+4x+5 2 x 3 − 3 x 2 + 4 x + 5 door x+2 met behulp van de lange afdeling algoritme.
Aanbevolen:
Hoe gebruik je trigonometrische verhoudingen om zijdelengtes te vinden?
In elke rechthoekige driehoek, voor elke hoek: De sinus van de hoek = de lengte van de overstaande zijde. de lengte van de hypotenusa. De cosinus van de hoek = de lengte van de aangrenzende zijde. de lengte van de hypotenusa. De tangens van de hoek = de lengte van de overstaande zijde. de lengte van de aangrenzende zijde
Zijn pesticiden allemaal synthetische chemicaliën?
Niet alleen dat, er is ook veel bewijs dat natuurlijke pesticiden die in de biologische landbouw zijn toegestaan, net zo giftig zijn als synthetische pesticiden. Synthetische chemicaliën zijn giftiger dan natuurlijke chemicaliën. 2. Biologisch geteeld voedsel is beter voor je omdat het allemaal natuurlijk is
Hoe gebruik je de waterverplaatsingsmethode om het volume van een onregelmatig object te vinden?
Plaats het object in de maatcilinder en noteer het resulterende watervolume als 'b'. Trek het volume van het water alleen af van het volume van het water plus het object. Als 'b' bijvoorbeeld 50 milliliter was en 'a' 25 milliliter, zou het volume van het onregelmatig gevormde object 25 milliliter zijn
Hoe gebruik je vermenigvuldiging om het quotiënt te vinden?
Bij vermenigvuldiging worden de getallen die je vermenigvuldigt factoren genoemd; het antwoord heet het product. Bij deling is het getal dat wordt gedeeld het deeltal, het getal dat het deelt is de deler en het antwoord is het quotiënt
Tijdens welke deling wordt het aantal chromosomen verminderd bij meiose?
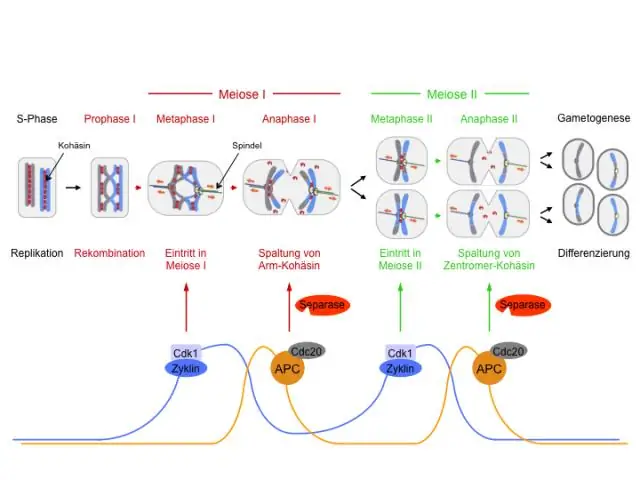
De eerste deling wordt de reductiedeling genoemd - of meiose I - omdat het het aantal chromosomen vermindert van 46 chromosomen of 2n tot 23 chromosomen of n (n beschrijft een enkele chromosoomset)