Inhoudsopgave:
Video: Hoe los je de coëfficiënt op door het kwadraat in te vullen?
2024 Auteur: Miles Stephen | [email protected]. Laatst gewijzigd: 2023-12-15 23:39
Nu kunnen we een kwadratische vergelijking in 5 stappen oplossen:
- Stap 1 Deel alle termen door a (de coëfficiënt van x2).
- Stap 2 Verplaats de getalterm (c/a) naar de rechterkant van de vergelijking.
- Stap 3 Voltooi het vierkant aan de linkerkant van de vergelijking en breng dit in evenwicht door dezelfde waarde toe te voegen aan de rechterkant van de vergelijking.
Wat zijn op deze manier coëfficiënten?
In de wiskunde, een coëfficiënt een multiplicatieve factor is in een term van een polynoom, een reeks of een andere uitdrukking; het is meestal een getal, maar kan elke uitdrukking zijn. Als y bijvoorbeeld wordt beschouwd als een parameter in de bovenstaande uitdrukking, is de coëfficiënt van x is −3y, en de constante coëfficiënt is 1,5 + j.
Ten tweede, wanneer kun je het vierkant niet voltooien? Trouwens, tenzij jij is verteld dat jij moet gebruiken Het vierkant voltooien , jij zal gebruik deze methode waarschijnlijk nooit in de praktijk bij het oplossen van kwadratische vergelijkingen. Ofwel een andere methode (zoals factoring) zullen wees duidelijk en sneller, of anders de kwadratische formule (hierna besproken) zullen gemakkelijker te gebruiken zijn.
Welke constante moet dus worden toegevoegd om het vierkant te voltooien?
De constante die moet worden toegevoegd en afgetrokken is (B) 1/64. wordt gebruikt om de kwadratische vergelijking op te lossen door de vierkant voltooien.
Wanneer moet ik het vierkant voltooien?
Vervolgens, als de coëfficiënt van de gekwadrateerde term 1 is en de coëfficiënt van de lineaire (middelste) term even, Het vierkant voltooien is een goede methode tot gebruik maken van. Ten slotte werkt de kwadratische formule op elke kwadratische vergelijking.
Aanbevolen:
Hoeveel kost het om een argontank te vullen?
Kost ongeveer $ 40 om te 'vullen'
Is zonde kwadraat x gelijk aan zonde x kwadraat?
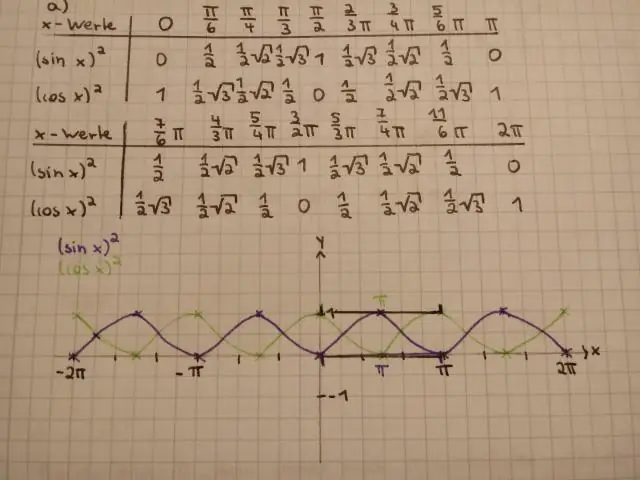
Jazeker. sin^2x is dezelfde assinx^2 omdat in beide gevallen de '^2' alleen betrekking heeft op de x
Hoe vind je de straal van een cirkel in het kwadraat?
Om het gebied van een cirkel met de straal te vinden, kwadrateert u de straal of vermenigvuldigt u deze met zichzelf. Vermenigvuldig vervolgens de gekwadrateerde straal met pi, of 3,14, om het gebied te krijgen. Om het gebied met de diameter te vinden, deelt u de diameter eenvoudig door 2, sluit u deze aan op de straalformule en lost u op zoals eerder
Wat zijn drie regels die het vullen van atomaire orbitalen door elektronen regelen?
Bij het toewijzen van elektronen aan orbitalen moeten we een reeks van drie regels volgen: het Aufbau-principe, het Pauli-uitsluitingsprincipe en de regel van Hund
Welke techniek zou een wetenschapper gebruiken om veel kopieën van een gewenst stukje DNA te maken om het lege tekstveld 1 in te vullen?
Moleculair klonen. Klonen maakt het mogelijk meerdere kopieën van genen te maken, genen tot expressie te brengen en specifieke genen te bestuderen. Om het DNA-fragment in een bacteriële cel te krijgen in een vorm die wordt gekopieerd of tot expressie wordt gebracht, wordt het fragment eerst in een plasmide ingebracht