Inhoudsopgave:
- Auteur Miles Stephen [email protected].
- Public 2024-01-18 08:17.
- Laatst gewijzigd 2025-01-22 17:06.
Er zijn drie stappen:
- Herschik de vergelijking zodat "y" aan de linkerkant staat en al het andere aan de rechterkant.
- Teken de "y="-lijn (maak er een ononderbroken lijn van voor y≤ of y≥, en een stippellijn voor y)
- Schaduw boven de lijn voor een "groter dan" (y> of y≥) of onder de lijn voor een "kleiner dan" (y< of y≤).
Hierin, hoe schaduw je ongewenste regio's?
Door schaduw de ongewenste regio's , toon de regio gedefinieerd door de verzameling ongelijkheden y < 2x + 5, y ≧ x, en x < 4. Oplossing: Teken de lijnen voor elk van de ongelijkheden en schaduw de ongewenste regio voor elk van hen.
Evenzo, hoe los je een stelsel van vergelijkingen op? Hier is hoe het gaat:
- Stap 1: Los een van de vergelijkingen voor een van de variabelen op. Laten we de eerste vergelijking voor y oplossen:
- Stap 2: Vervang die vergelijking door de andere vergelijking en los op voor x.
- Stap 3: Vervang x = 4 x = 4 x=4 in een van de oorspronkelijke vergelijkingen en los op voor y.
Evenzo, hoe vind je de ongelijkheid?
We kunnen ongelijkheden vaak oplossen door een getal van beide kanten op te tellen (of af te trekken) (net als in Inleiding tot Algebra), zoals dit:
- Los op: x + 3 < 7. Als we 3 van beide kanten aftrekken, krijgen we:
- Los op: 3y < 15. Als we beide zijden door 3 delen, krijgen we:
- Oplossen: −2y < −8.
- Oplossen: bx < 3b.
Wat is de ongelijkheid?
Een ongelijkheid vergelijkt twee waarden en laat zien of een kleiner dan, groter dan of gewoon niet gelijk is aan een andere waarde. a ≠ b zegt dat a niet gelijk is aan b. een b zegt dat a groter is dan b. (die twee staan bekend als strikte ongelijkheid) )
Aanbevolen:
Hoe vind je de onderscheppingen van een ongelijkheid?
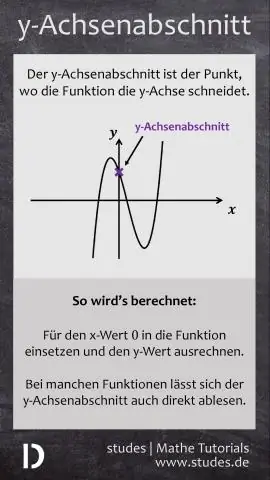
Als alternatief kunnen we het x-snijpunt en het y-snijpunt van de standaardvorm lineaire ongelijkheid bepalen door y = 0 te substitueren, vervolgens op te lossen voor x en te vervangen door x = 0 en vervolgens op te lossen voor y respectievelijk. Bedenk dat het x-snijpunt de waarde is van x wanneer y = 0 en zij-snijpunt is de waarde van y wanneer x = 0
Hoe bepaal je of een ongelijkheid geen oplossing heeft?

Isoleer de absolute waarde-uitdrukking aan de linkerkant van de ongelijkheid. Als het getal aan de andere kant van het ongelijkheidsteken negatief is, heeft je vergelijking geen oplossing of alle reële getallen als oplossingen. Gebruik het teken van elke kant van je ongelijkheid om te beslissen welke van deze gevallen geldt
Hoe schrijf je het domein van een ongelijkheid?

Als ongelijkheid zouden we Read schrijven als 'het domein van de functie zijn alle waarden van x die groter zijn dan of gelijk zijn aan nul'. Zie Ongelijkheden voor meer informatie over ongelijkheden. In de zogenaamde intervalnotatie heeft dezelfde functie een domein van Dit beschrijft de reeks waarden van 0 tot positief oneindig
Hoe los je een vergelijking of ongelijkheid op?

Gebruik de volgende stappen om een ongelijkheid op te lossen: Stap 1 Elimineer breuken door alle termen te vermenigvuldigen met de kleinste gemene deler van alle breuken. Stap 2 Vereenvoudig door gelijke termen aan elke kant van de ongelijkheid te combineren. Stap 3 Optellen of aftrekken van hoeveelheden om het onbekende aan de ene kant en de getallen aan de andere kant te krijgen
Hoe weet je of een absolute waarde-ongelijkheid geen oplossing heeft?

Oké, als absolute waarden altijd positief of nul zijn, kunnen ze op geen enkele manier kleiner zijn dan of gelijk zijn aan een negatief getal. Daarom is er voor geen van beide een oplossing. In dit geval, als de absolute waarde positief of nul is, is deze altijd groter dan of gelijk aan een negatief getal
