
Inhoudsopgave:
- Auteur Miles Stephen stephen@answers-science.com.
- Public 2023-12-15 23:39.
- Laatst gewijzigd 2025-06-01 05:05.
Vermenigvuldiging en samenstelling van functies
- Tot vermenigvuldigen een functie door een scalair, vermenigvuldigen elke output door die scalair.
- Als we f (g(x)) nemen, nemen we g(x) als invoer van de functie F.
- Bijvoorbeeld, als f (x) = 10x en g(x) = x + 1, dan vinden we f (g(4)), g(4) = 4 + 1 + 5, en evalueren dan f (5) = 10(5) = 50.
- Voorbeeld: f (x) = 2x - 2, g(x) = x2 - 8.
Dienovereenkomstig, hoe voer je meerdere functies uit?
Vermenigvuldiging van Functies Tot vermenigvuldigen een functie door iemand anders functie , vermenigvuldigen hun uitgangen. Bijvoorbeeld, als f (x) = 2x en g(x) = x + 1, dan is fg(3) = f (3)×g(3) = 6×4 = 24. fg(x) = 2x(x + 1) = 2x2 +x.
Bovendien, hoe teken je een functie? Houd rekening met de functie f(x) = 2 x + 1. We herkennen de vergelijking y = 2 x + 1 als de helling-snijvorm van de vergelijking van een lijn met helling 2 en y-snijpunt (0, 1). Denk aan een punt dat beweegt op de grafiek uit. Naarmate het punt naar rechts beweegt, stijgt het.
Vervolgens kan men zich ook afvragen: wat is het product van twee functies?
Wanneer je vermenigvuldigt twee functies: samen krijg je een derde functie als resultaat, en dat derde functie zal de zijn Product van de twee origineel functies . Als u bijvoorbeeld f(x) en g(x) vermenigvuldigt, is hun Product zal h(x)=fg(x), of h(x)=f(x)g(x) zijn. Je kunt ook de Product op een bepaald punt.
Hoe los je een functie op?
Voor functies , betekenen de twee notaties precies hetzelfde, maar "f (x)" geeft je meer flexibiliteit en meer informatie. Je zei altijd "y = 2x + 3; oplossen voor y als x = -1". Nu zeg je "f (x) = 2x + 3; find f (-1)" (uitgesproken als "f-of-x is gelijk aan 2x plus drie; vind f-of-negative-one").
Aanbevolen:
Hoe evalueer je samengestelde functies?
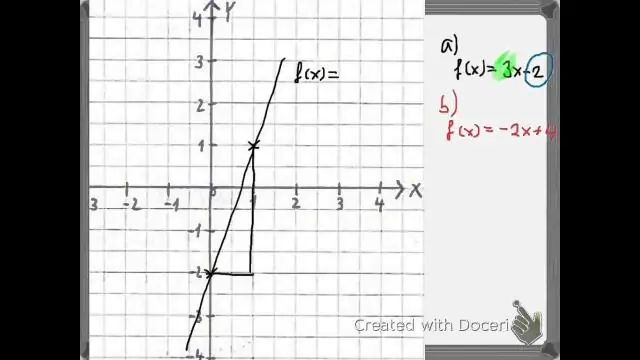
Samengestelde functies evalueren met behulp van grafieken Lokaliseer de gegeven invoer voor de binnenste functie op de x-as van zijn grafiek. Lees de uitvoer van de binnenfunctie af van de y-as van zijn grafiek. Zoek de uitvoer van de binnenste functie op de x-as van de grafiek van de buitenste functie
Hoe doe je waarschijnlijkheid samengestelde gebeurtenissen?
Het bepalen van de waarschijnlijkheid van een samengestelde gebeurtenis omvat het vinden van de som van de kansen van de afzonderlijke gebeurtenissen en, indien nodig, het verwijderen van overlappende kansen. Een exclusieve samengestelde gebeurtenis is een gebeurtenis waarin de meerdere gebeurtenissen elkaar niet overlappen. In wiskundige termen: P(C) = P(A) + P(B)
Hoe kan een model helpen bij het vinden van de waarschijnlijkheid van een samengestelde gebeurtenis?
Definitie van waarschijnlijkheid van samengestelde gebeurtenissen Een samengestelde gebeurtenis is een gebeurtenis waarbij er meer dan één mogelijke uitkomst is. Het bepalen van de waarschijnlijkheid van een samengestelde gebeurtenis omvat het vinden van de som van de kansen van de afzonderlijke gebeurtenissen en, indien nodig, het verwijderen van overlappende kansen
Waarom worden trigonometrische functies circulaire functies genoemd?

Goniometrische functies worden soms circulaire functies genoemd. Dit komt omdat de twee fundamentele trigonometrische functies - de sinus en de cosinus - worden gedefinieerd als de coördinaten van een punt P dat rondloopt op de eenheidscirkel met straal 1. De sinus en de cosinus herhalen hun output met regelmatige tussenpozen
Hoe vermenigvuldig je rationale functies?

Q en S zijn niet gelijk aan 0. Stap 1: Factor zowel de teller als de noemer. Stap 2: Schrijf als één breuk. Stap 3: Vereenvoudig de rationele uitdrukking. Stap 4: Vermenigvuldig eventuele resterende factoren in de teller en/of noemer. Stap 1: Factor zowel de teller als de noemer. Stap 2: Schrijf als één breuk
