Video: Hoe gebruik je de product- en quotiëntregel?
2024 Auteur: Miles Stephen | [email protected]. Laatst gewijzigd: 2023-12-15 23:39
De Productregel zegt dat de afgeleide van a Product van twee functies is de eerste functie maal de afgeleide van de tweede functie plus de tweede functie maal de afgeleide van de eerste functie. De Productregel moet worden gebruikt wanneer de afgeleide van de quotiënt van twee functies moet worden genomen.
Wat is daarnaast de formule voor de productregel?
De productregel is een formule gebruikt om de afgeleiden van te vinden producten van twee of meer functies. (uv)'=u'v+uv'. Δ(uv)=u(x+Δx)v(x+Δx)−u(x)v(x). waarbij Δu en Δv respectievelijk de incrementen zijn van de functies u en v.
Bovendien, wat is de productregel voor exponenten? De exponent "productregel" vertelt ons dat, wanneer je twee machten met hetzelfde grondtal vermenigvuldigt, je de exponenten kunt optellen. In dit voorbeeld zie je hoe het werkt. Het toevoegen van de exponenten is slechts een kortere weg! De " machtsregel " vertelt ons dat om een macht tot een macht te verheffen, gewoon… vermenigvuldigen de exponenten.
Wat is in dit verband de quotiëntregel voor exponenten?
Quotiëntregel:, dit zegt dat tot verdeling twee exponenten met hetzelfde grondtal, je behoudt het grondtal en aftrekken de bevoegdheden. Dit is vergelijkbaar met het reduceren van fracties; wanneer je aftrekken de machten zetten het antwoord in de teller of noemer, afhankelijk van waar de hogere macht zich bevond.
Wat is de afgeleide van 1?
De Derivaat vertelt ons de helling van een functie op elk punt. Er zijn regels die we kunnen volgen om er veel te vinden derivaten . Bijvoorbeeld: De helling van een constante waarde (zoals 3) is altijd 0.
Derivaat Reglement.
| Algemene functies | Functie | Derivaat |
|---|---|---|
| Constante | C | 0 |
| Lijn | x | 1 |
| bijl | een | |
| Vierkant | x2 | 2x |
Aanbevolen:
Hoe weet je wanneer je de product- of quotiëntregel moet gebruiken?
Functieverdeling. Dus, wanneer je vermenigvuldiging van twee functies ziet, gebruik de productregel en in geval van deling de quotiëntregel. Als de functie zowel vermenigvuldigen als delen heeft, gebruik dan beide regels dienovereenkomstig. Als je een algemene vergelijking ziet, is het zoiets als,, waar is een functie in termen van alleen
Hoe gebruik je de rechterhandregel voor cross-product?
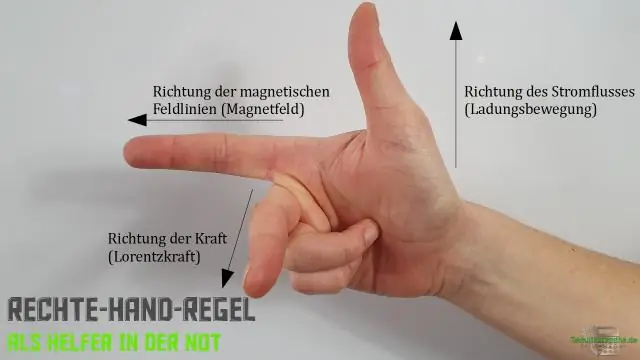
De rechterhandregel stelt dat de oriëntatie van het uitwendige product van de vectoren wordt bepaald door het plaatsen en staart-aan-staart, de rechterhand plat te maken, uit te strekken in de richting van, en dan de vingers te krullen in de richting waarmee de hoek wordt gemaakt. De duim wijst dan in de richting van
Hoe zet je de quotiëntregel om in een productregel?
De quotiëntregel zou kunnen worden gezien als een toepassing van de product- en ketenregels. Als Q(x) = f(x)/g(x), dan is Q(x) = f(x) * 1/(g(x)). U kunt de productregel gebruiken om Q(x) te differentiëren, en de 1/(g(x)) kan worden onderscheiden met een kettingregel met u = g(x), en 1/(g(x)) = 1/u
Wanneer gebruik je de activiteitenreeks hoe gebruik je hem?
Het wordt gebruikt om de producten van enkelvoudige verplaatsingsreacties te bepalen, waarbij metaal A een ander metaal B in een oplossing zal vervangen als A hoger in de reeks is. Activiteitenreeksen van enkele van de meest voorkomende metalen, gerangschikt in aflopende volgorde van reactiviteit
Kun je de productregel gebruiken in plaats van de quotiëntregel?
Er zijn twee redenen waarom de quotiëntregel superieur kan zijn aan de machtsregel plus productregel bij het differentiëren van een quotiënt: Het behoudt gemeenschappelijke noemers bij het vereenvoudigen van het resultaat. Als u de machtsregel plus de productregel gebruikt, moet u vaak een gemeenschappelijke noemer vinden om het resultaat te vereenvoudigen