Video: Hoe vind je denkbeeldige wortels met de tekenregel van Descartes?
2024 Auteur: Miles Stephen | [email protected]. Laatst gewijzigd: 2023-12-15 23:39
De tekenregel van Descartes zegt het aantal positieve wortels is gelijk aan veranderingen in teken van f(x), of kleiner is dan een even getal (dus je blijft 2 aftrekken totdat je 1 of 0 krijgt). Daarom kan de vorige f(x) 2 of 0 positief hebben wortels . Negatief echt wortels.
Mensen vragen zich ook af: wat zegt de tekenregel van Descartes je over de echte wortels van de veelterm?
Descartes ' regel van teken. Descartes ' regel van teken wordt gebruikt om bepalen het aantal echt nullen van a polynoom functie. Het vertelt ons dat het aantal positieve echt nullen in a polynoom functie f(x) is gelijk aan of kleiner dan een even getal als het aantal veranderingen in het teken van de coëfficiënten.
Weet ook, hoeveel echte wortels heeft een polynoom? Als we tellen wortels volgens hun veelvoud (zie De Factorstelling), dan: A polynoom van graad n can hebben alleen een even getal kleiner dan n echte wortels . Dus, wanneer we multipliciteit tellen, een kubieke polynoom kan hebben alleen drie wortels of een wortel ; een kwadratische polynoom kan hebben enkel twee wortels of nul wortels.
Hiervan, wat is een echte nul?
Echte nullen . Bedenk dat een echte nul is waar een grafiek de x-as kruist of raakt. Denk aan enkele punten langs de x-as.
Hoeveel wortels heeft een vergelijking?
een kwadratische vergelijking met reële coëfficiënten kan hebben ofwel een of twee verschillende echte wortels , of twee verschillende complexe wortels . In dit geval bepaalt de discriminant het aantal en de aard van de wortels . Er zijn drie gevallen: als de discriminant positief is, zijn er twee verschillende wortels.
Aanbevolen:
Hoe los je de tekenregel van Descartes op?
De tekenregel van Descartes vertelt ons dat we dan precies 3 reële positieve nullen of minder hebben, maar een oneven aantal nullen. Daarom moet ons aantal positieve nullen dan ofwel 3 of 1 zijn. Hier kunnen we zien dat we twee tekenveranderingen hebben, dus we hebben twee negatieve nullen of minder, maar een even aantal nullen
Hoe vind je de tegenovergestelde zijde van een driehoek met behulp van Pythagoras?
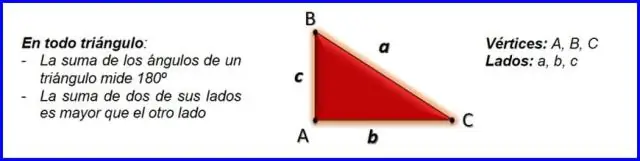
Rechte driehoeken en de stelling van Pythagoras De stelling van Pythagoras, a2+b2=c2, a 2 + b 2 = c 2, kan worden gebruikt om de lengte van elke zijde van een rechthoekige driehoek te bepalen. De zijde tegenover de rechte hoek wordt de hypotenusa genoemd (zijde c in de figuur)
Hoe vind je de discriminant en de aard van wortels?
De discriminant (EMBFQ) Dit is de uitdrukking onder de vierkantswortel in de kwadratische formule. De discriminant bepaalt de aard van de wortels van een kwadratische vergelijking. Het woord 'natuur' verwijst naar de soorten getallen die de wortels kunnen zijn - namelijk echt, rationeel, irrationeel of denkbeeldig
Hoe vind je de wortels van een vergelijking algebraïsch?
De wortels van elke kwadratische vergelijking worden gegeven door: x = [-b +/- sqrt(-b^2 - 4ac)]/2a. Noteer de kwadratische vorm in de vorm van ax^2 + bx + c = 0. Als de vergelijking in de vorm y = ax^2 + bx +c is, vervang dan gewoon de y door 0. Dit wordt gedaan omdat de wortels van de vergelijking zijn de waarden waarbij de y-as gelijk is aan 0
Waarom is het belangrijk om rekening te houden met multipliciteit bij het bepalen van de wortels van een polynoomvergelijking?
Het aantal keren dat een gegeven polynoomvergelijking bijvoorbeeld een wortel heeft op een bepaald punt, is de veelvoud van die wortel. Het begrip multipliciteit is belangrijk om correct te kunnen tellen zonder uitzonderingen te specificeren (bijvoorbeeld dubbele wortels dubbel geteld). Vandaar de uitdrukking, 'geteld met veelvoud'