
- Auteur Miles Stephen [email protected].
- Public 2023-12-15 23:39.
- Laatst gewijzigd 2025-01-22 17:06.
richtlijn . EEN parabool is een verzameling van alle punten in een vlak die op gelijke afstand van een bepaald punt en een gegeven lijn liggen. Het punt wordt het brandpunt van de genoemd parabool , en de lijn heet de richtlijn . De richtlijn staat loodrecht op de symmetrieas van a parabool en raakt de niet aan parabool.
Bovendien, hoe vind je de Directrix van een parabool?
De standaardvorm is (x - h)2 = 4p (y - k), waarbij de focus is (h, k + p) en de richtlijn is y = k - p. Als de parabool is geroteerd zodat het hoekpunt (h, k) is en de symmetrieas evenwijdig is aan de x-as, het heeft een vergelijking van (y - k)2 = 4p (x - h), waarbij de focus is (h + p, k) en de richtlijn is x = h - p.
En hoe vind je de topvorm van een parabool? f (x) = a(x - h)2 + k, waarbij (h, k) de. is hoekpunt van de parabool . Ter info: verschillende leerboeken hebben verschillende interpretaties van de verwijzing "standaard" formulier " van een kwadratische functie. Sommigen zeggen f (x) = ax2 + bx + c is "standaard formulier ", terwijl anderen zeggen dat f (x) = a(x - h)2 + k is "standaard" formulier ".
Evenzo kan men zich afvragen, wat is de richtlijn van een hyperbool?
In het geval van een hyperbool , een richtlijn is een rechte lijn waarbij de afstand van elk punt op de hyperbool tot een van zijn twee brandpunten is maal de loodrechte afstand van tot de richtlijn , waarbij een constante groter is dan. Let daar op hyperbolen hebben twee brandpunten en twee richtlijnen, één voor elk brandpunt.
Hoe vind je de richtlijn van een vergelijking?
De standaardvorm is (x - h)2 = 4p (y - k), waarbij de focus is (h, k + p) en de richtlijn is y = k - p. Als de parabool zo wordt geroteerd dat het hoekpunt (h, k) is en de symmetrieas evenwijdig aan de x-as, heeft deze een vergelijking van (y - k)2 = 4p (x - h), waarbij de focus is (h + p, k) en de richtlijn is x = h - p.
Aanbevolen:
Wat voor soort vergelijking is een parabool?

De standaardvorm is (x - h)2 = 4p (y - k), waarbij het brandpunt (h, k + p) is en de richtlijn y = k - p is. Als de parabool zo wordt geroteerd dat het hoekpunt (h,k) is en de symmetrieas evenwijdig is aan de x-as, heeft deze een vergelijking van (y - k)2 = 4p (x - h), waarbij het brandpunt is (h + p, k) en de richtlijn is x = h - p
Is de boog van Saint Louis een parabool?

Dit artikel heeft aangetoond dat de Gateway Arch geen parabool is. Het heeft eerder de vorm van een afgeplatte (of verzwaarde) bovenleiding, wat de vorm is die we zien als we een ketting ophangen die dun is in het midden tussen twee vaste punten
Wat is het maximum of minimum punt van een parabool?

Verticale parabolen geven een belangrijk stuk informatie: wanneer de parabool zich opent, is het hoekpunt het laagste punt op de grafiek - het minimum of min genoemd. Wanneer de parabool naar beneden opent, is het hoekpunt het hoogste punt op de grafiek - het maximum of max
Hoe teken je een kegelsnede van een parabool?
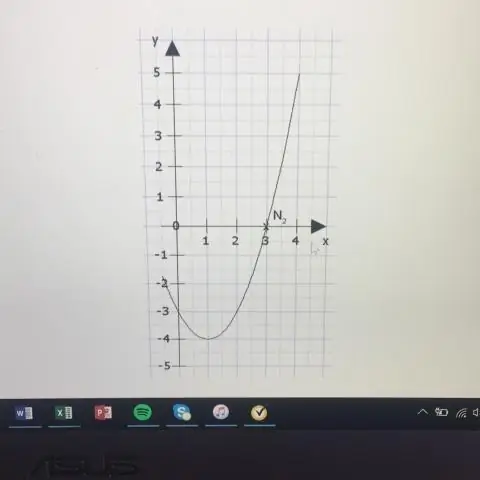
De richtlijn is de lijn y = k - p. De as is de lijn x = h. Als p > 0, opent de parabool naar boven, en als p < 0, opent de parabool naar beneden. Als een parabool een horizontale as heeft, is de standaardvorm van de vergelijking van de parabool deze: (y - k)2 = 4p(x - h), waarbij p≠ 0
Hoe maak je een kegelsnede van een parabool?
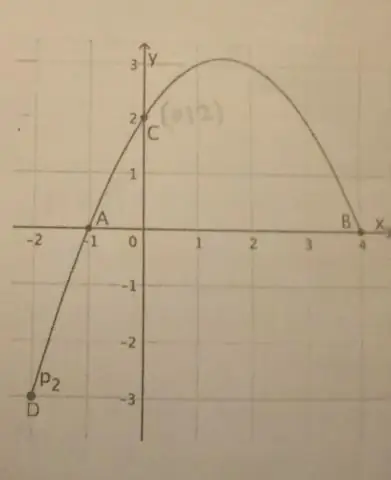
Als een parabool een verticale as heeft, is de standaardvorm van de vergelijking van de parabool deze: (x - h)2 = 4p(y - k), waarbij p≠ 0. Het hoekpunt van deze parabool is op (h, k). De focus ligt op (h, k + p). De richtlijn is de lijn y = k - p
